S'il n'y avait que deux observateurs dans un monde parfait, l'analyse, pour déterminer où se trouve le début d'un météore par exemple, reviendrait à trouver un point dans l'espace qui se situe au croisement de deux droites. Droites qui seraient les lignes de visée des deux observateurs.

Or, le monde n'est pas parfait et il y a toutes les chances du monde pour que les deux lignes de visé ne se croisent pas. En effet, dans un espace en trois dimensions, deux droites ne se croisent pas forcément. De surcroît, il y a plus que deux observateurs.

Le problème revient donc à trouver un point dans l'espace qui soit le plus près possible de toutes les lignes de visée. Je reviendrai plus tard à cette technique. Pour l'instant, concentrons-nous sur le référentiel utilisé pour localiser tous les intervenants (le système de référence pour les coordonnées).

Imaginons un système de trois axes perpendiculaires x, y et z dans l'espace; voir la figure 1.

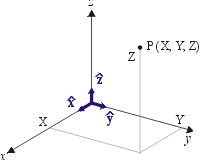
Figure 1

 Nous pouvons localiser le point P dans cet espace à l'aide des coordonnées X, Y, Z. Imaginons également, dans ce système, trois vecteurs unitaires , et . De manière vectorielle, nous pourrons alors décrire le point P comme suit:

Nous pouvons également localiser le même point P à l'aide des coordonnées sphériques; voir la figure 2: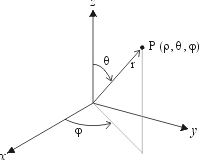

Figure 2

Qu'en est-il maintenant d'une droite dans cet espace? Imaginons qu'un observateur est situé au bout du vecteur On sur la figure 3: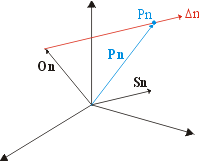

Figure 3

Cet observateur voit apparaître une étoile filante dans la direction du segment de droite. pointe vers une étoile quelconque qui possède des coordonnées connues. Si le système d'axes a pour origine le centre de la Terre, alors un vecteur qui pointerait vers l'étoile dont il est question serait parallèle à . C'est le cas du vecteur Sn.

Imaginons que nous voulions localiser un point Pn sur la droite à l'aide du vecteur Pn. Comme est parallèle à Sn, un vecteur (non illustré) qui irait de l'observateur jusqu'au point Pn serait proportionnel à Sn. On peut donc dire que le vecteur Pn peut être décrit de la manière suivante:

Où Kn est une constante de proportionnalité. Cette équation est une équation paramétrique vectorielle. En jouant avec la constante Kn, on engendre tous les points de la droite . Un paramètre scalaire permet donc de se promener dans l'espace … en autant qu'on reste sur !

Revenons au référentiel, le système d'axes. On a dit qu'il prenait son origine au centre de la Terre. Nous allons l'orienter de la manière suivante; voir figure 4.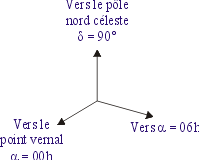

Fugure 4

Le vecteur Sn est facile à positionner dans ce référentiel. On aura la concordance suivante entre les coordonnées sphériques et les coordonnées équatoriales (alpha = AD et delta = déclinaison):

Ici, et pour la suite, il est important de considérer toutes les grandeurs angulaires en radians. Pour ce faire, utilisez la méthode suivante:

AD ou heure sidérale sous la forme HH:MM:SS en radians =

Pi * ( HH * 3600 + MM * 60 + SS ) / 43200

DEC, Longitude ou Latitude sous la forme DDMMSS en radians =

Pi * (DD * 3600 + MM * 60 + SS ) / 648000

Pour le vecteur On, c'est légèrement plus compliqué. En effet, l'observateur est fixe sur la Terre, mais comme la Terre tourne durant la nuit, il va se déplacer dans le référentiel. Toutefois, la latitude de l'observateur est indépendante du temps. Pour régler le problème de la longitude, nous allons utiliser l'heure sidérale des observations. En utilisant l'heure sidérale de l'observation (HSn) plutôt que la longitude, nous avons un système qui est parfaitement conforme avec le référentiel choisi. La longueur r (coor. Sphériques) de On est le rayon de la Terre plus l'altitude de l'observateur. J'utiliserai comme rayon terrestre 6378km. Nous avons donc:

Où hn est l'altitude (en km) de l'observateur.

Nous allons maintenant exprimer l'équation paramétrique vectorielle de la droite en coordonnées rectangulaires:

Voici comment transformer les vecteurs On en coordonnées rectangulaires (et c'est le même raisonnement pour Sn):

Maintenant que nous avons tous les outils pour paramétriser un observateur, attaquons-nous au cœur du problème. Imaginons que nous avons un nombre N d'observateurs qui voient un même météore apparaître en un point de leur ciel respectif. Chacun voit ce point le long d'une droite qui lui est propre. Nous cherchons à trouver un point P qui soit le plus près possible de toutes ces droites à la fois (Dans un monde parfait, le point P serait au sommet d'une espèce de cône engendré par toutes les droites).

Pour trouver ce point P situé à X, Y, Z dans l'espace, nous allons définir une grandeur Dn qui sera la distance entre le point P et un point quelconque (engendré par le paramètre Kn ) sur une droite . Donc:

Nous allons maintenant sommer (additionner) tous les Dn obtenus pour chaque droite :