4. PRODUCING THE FLAT-FIELD MAP
The sequence of raw flat-field images was obtained during sunset with increasing integration times. We choosed these integration times so that about half the dynamic range of the camera is used for each exposure (here between 10 and 20 seconds).
Note: To get information at any time about the image in memory, just type:
INFO

By looking at any of the images, one may note that there are several stars in each of them. To eliminate the stars, the median method is once more the best one. However, to realize the median average, we must first correct the images from their individual dark current map, their offset, and then normalize each image to a common mean level, so that it simulates images taken in homogeneous conditions.
A classic solution is to take an exposure of the object under study with an integration time T, then to take another exposure of length T while placing the detector in total darkness. This last exposure is called the dark current map. This map is a constant, to within a coefficient, for a given CCD. To first order, the coefficient is proportional to the temperature of the CCD and to the integration time. In the preceding procedure, the dark current map is simply subtracted from the image of the object.
This is, however, far from the ideal solution. In fact, this procedure implies that a dark current map must be taken after each image of the object. This is very constraining when the exposure time is several minutes or more.
Things seem to go better if the temperature of the CCD is perfectly stable. In this case, a priori only one map is necessary. It can be taken, for example, at the beginning of the observing session, and can be used to correct all the images. If the exposure time is not the same on the dark map and the image to be processed, the dark map must be multiplied by a coefficient before the subtraction. The coefficient is the ratio of the exposure time of the image to the exposure time of the dark map.
Besides the fact that it is a delicate matter to maintain the detector at a fixed temperature, this method has the following inconvenience - the dark map has its own noise (readout noise) and when the map is subtracted from the images, this noise is actually added to the images.
There is a more efficient technique: it is an iterative method that automatically determines the optimal coefficient to be used when multiplying the dark map.
A portion of the dark current map, which has been multiplied by an arbitrary coefficient, is subtracted from the corresponding portion of the image to be processed.
The result is likely to be mediocre and the output image noisy, since the acquisition conditions of the two images are not the same (different integration times, different temperatures). Another subtraction will be performed with a new value for the coefficient, for example, a smaller one. If the residual noise is attenuated, this means that it is going in the right direction.
This process continues in order to obtain the minimal residual noise (if the calculations are continued in the same direction the noise will increase again). The OPT command finds this minimum in the noise curve.
Note: In Iris we use an analytical approach that reproduces this iterative method with a much faster result.
Load the first image in memory:
LOAD F_1
Define a small rectangular zone with the mouse around a hot-pixel, and then type:
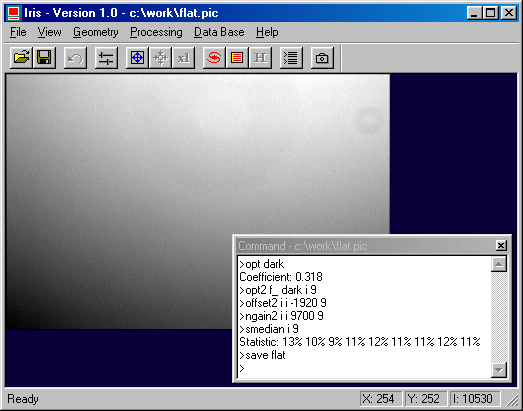
OPT DARK
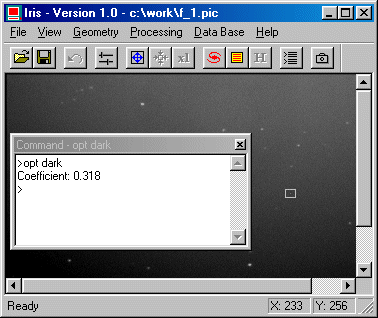
Iris will compute the optimization of the dark map in the selected area. The parameter of the OPT command refers to the image name of the dark current map (here, DARK.PIC). Iris will return the value of the coefficient to be used for the multiplication before subtracting the dark map. Here the result should be close to 0.318 (this near the ratio of exposure time for F_1 image and for DARK image, i.e. 20s/60s=0.333).
Then, the dark map may be subtracted from the first image:
LOAD DARK
MULT 0.318
SAVE N
LOAD F_1
SUB N 0
The MULT command has multiplied each pixel of the DARK image by 0.318, then the result was saved inder the file N, that is subtracted from the image F_1.PIC.
Lastly, don't forget to subtract also the offset map:
SUB OFFSET 0
SAVE I1
The result image is called I1 (file I1.PIC on disk). The same work should be made for the remaining 8 images. That may become a little boring to do for a large number of images, so a better method is to use the OPT2 command:
OPT2 F_ DARK I 9
For this select the same zone in the first image of the sequence frame (F_1). The first parameter of OPT is the generic name of the images to be processed. The following ones is the name of the dark current map. The 3th one is the generic name of the result image, and the last parameter is the number of images to be processed. Here, 9 images from I1.PIC to I9.PIC will be created onto your hard drive.
Now subtract the offset map of the I flat-field images (OFFSET2 command):
OFFSET2 I I -1920 9
The first parameter is the generic name of the images to be processed, whereas the second parameter is the generic name of the output images (here, we have chosen the same filename for the input and output files, so that we preserve disk space, because the input images will not be used anymore. Be always careful before choosing to overwrite some of your files!!!). The 3rd parameter is the offset level (note the negative value), and the last parameter is of course the number of images to process.

Before combining these image with the median method, we still have to normalize them. We will then multiply each of them with a given factor so that their mean (in fact, median) level becomes a constant for each image. Here, let's choose a final level of 9700 (this is about the level in each of the images I1 to I9). Type:
NGAIN2 I I 9700 9
The first parameter of NGAIN2 is the generic name of the images to be processed, whereas the second parameter is the generic name of the output images. The 3rd parameter is the median level to obtain after processing, and the last parameter is of course the number of images to process.
The last operation is the median combining of the sequence I1.PIC...I9.PIC:
SMEDIAN I 9
SAVE FLAT
Looking at the result will show you that both stars and cosmic rays have disappeared.