Le SHACK HARTMANN

Qu'est ce qu'un Shack Hartmann ?

C'est un optique système inventé en 1971, à partir de la méthode de Hartmann inventée elle même en 1900. Il est dédié au contrôle métrologique des optiques, par la reconstruction d'un front d'onde incident dans un système optique. Cette méthode est maintenant utilisée en optique adaptative pour mesurer les distorsions d'un front d'onde par la turbulence en temps réel. Par rapport à la méthode de Hartmann, c'est une méthode plus précise. Elle permet d'utiliser des étoiles plus faibles, parce que le système de Shack Hartmann utilise toute la pupille, ce qui n'est pas le cas du Test Hartmann où le nombre de trous ou de sous pupilles est limité sur deux axes.

Quelques notions de base :

C'est la combinaison des deux effets d'altération du front d'onde par le système optique et par la turbulence qui produisent des images de mauvaise qualité au foyer de nos télescopes. La turbulence est prépondérante pour des sites de plaine dés que le diamètre de l'instrument fait plus de 100mm.

Le Shack-Hartmann permet de mesurer les deux effets indépendamment, et ce, avec une très bonne précision :

Il permet donc :

 


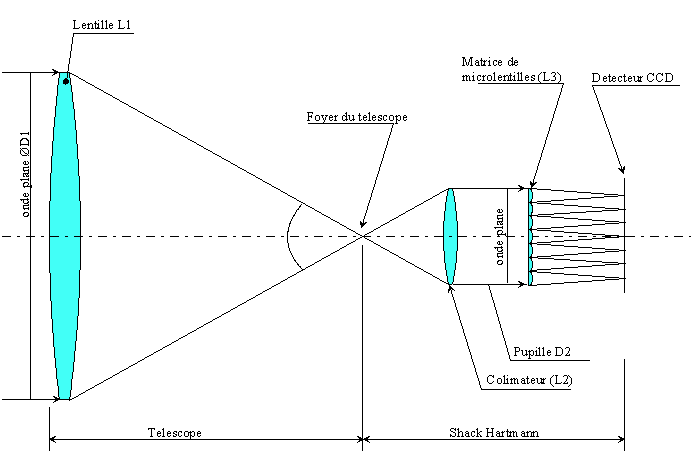
Figure 1

La figure 1 montre le principe du Shack hartmann :
Une onde plane de diamètre D1 entre dans le télescope, elle est représenté schématiquement par une lentille L1, les faisceaux convergent tous vers le foyer, on supposera que notre système optique est parfait, c'est à ce point que fini le télescope, et que commence le Shack hartmann. Ce dernier est constitué d'un collimateur de très bonne qualité, qui transforme le système en un système afocal, c'est à dire produit des faisceaux parallèles, à ce niveau le front d'onde est de nouveau plan. Cette fonction peut être facilement réalisée par un oculaire, il produit un front d'onde plan qui arrive sur l'œil lorsque l'on observe. On a ainsi re-imagé la pupille D1 d'entrée du télescope en une pupille réduite D2. Ensuite, une matrice de microlentilles L3 sera placée sur le chemin, son but est de découper la pupille D2 en sous pupilles. Comme le front d'onde au niveau de la pupille D2 est plan, la matrice de microlentilles fait converger le faisceau en une matrice de spots, à la distance focale des dites micro lentilles.

 


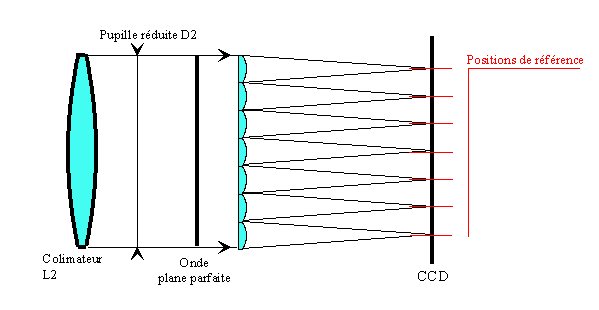
Figure 2

La figure 2, montre plus en détail ce qui se passe à partir du foyer du télescope.
Le front d'onde de la pupille D2 est plat, et les faisceaux convergeant forment sur l'image une matrice de spots bien régulièrement espacé. La position de référence en X et en Y de chaque spot sur la matrice CCD est mesuré, grâce à des algorithmes, la mesure de position des spots peut se réaliser à mieux que le 1/50ieme de pixels.

 


Figure 2a : Image CCD webcam (en négatif) , de spots issus d'une matrice de microlentilles, au foyer un trou de 10µm a été placé, la position de ces spots donnent la position de référence, cette calibration est réalisé une fois pour toutes si le système n'est pas désassemblé.

 


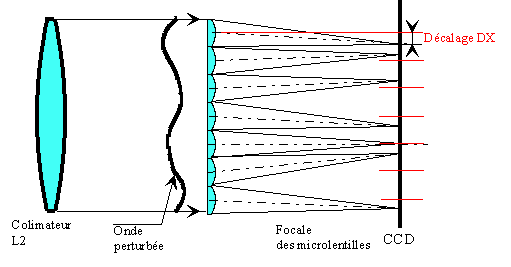
Figure 3


Si le front d'onde au niveau de la pupille D2 est distordu (figure 3) soit par les défauts optiques, ou soit par la turbulence, en passant à travers la matrice de microlentilles, la position des spots va être changée : on admet que localement au niveau de la microlentille, le front d'onde est un front d'onde plan, mais incliné d'une certaine valeur. C'est l'assemblage de tout ces sous front d'ondes plan locaux et de leur pente qui constitue l'ensemble du front d'onde de la pupille D2. En mesurant l'écart Dx et Dy (dans la direction orthogonale) pour chaque spot par rapport à la position de référence que l'on arrive à reconstituer tout le front d'onde. En fait le shack Hartmann mesure la dérivée première du front d'onde. La reconstruction du front d'onde est une opération mathématique relativement classique, et à la portée des ordinateur actuels.
Cette reconstruction du front d'onde est basé sur une famille de fonctions mathématiques, dites polynômes de Zernikes. C'est une famille de fonctions orthogonales sur le cercle unité. Il en existe d'autres comme les polynômes de Seidel etc… On peut reconstruire mathématiquement le front d'onde grâce à une combinaison linéaire de polynôme de Zernike Z0,Z1...ZN et de leur coefficient associé a0,a1..aN. (voir ici sur les fonctions de Zernikes, c'est trés bien fait)

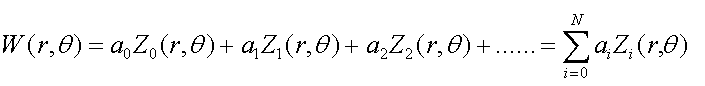Eq 1

- r entre 0 et 1
- Teta entre 0 et 2Pi
Plus le numéro du polynôme de Zernike a un d'indice élevé, plus il traduit des aberrations d'ordre élevé, et aussi des formes d'ondes de plus en plus complexes.

Ce qui est bien utile, avec cette famille de polynômes, c'est qu'ils représentent des aberrations optiques indépendantes les unes des autres. Le coefficient (a1) devant le polynôme Z1 représente un Tilt sur l'axe des X qui n'a rien a avoir avec le coefficient (a2) devant Z2 qui représente un Tilt sur l'axe des Y, le coefficient devant Z3 représente (a3) le défocus qui n'a rien avoir avec a1 et a2. On peut donc séparer les aberrations les unes des autres.

On appelle cette reconstruction du front d'onde par polynômes de Zernike, la méthode de reconstruction modale.


Quelle précision peut on attendre ?

Il est intéressant de connaître la déviation des spots pour des écarts de front d'onde connus : une simulation a été réalisée à cet effet.

Il a été pris une taille de pixel de 5.6µm (pixel d'une webcam), un diamètre de chaque microlentille de 130µm et une focale de microlentille de 5mm. Une aberration Z8, aberration de sphéricité du 3ieme ordre, a été retenue pour ce test (c'est une aberration de révolution)

Figure 4 : Front d'onde vu de face (Z8, aberration de sphéricité du 3ieme ordre) , en clair les parties en avance de phase, en noir, les parties en retard de phase.

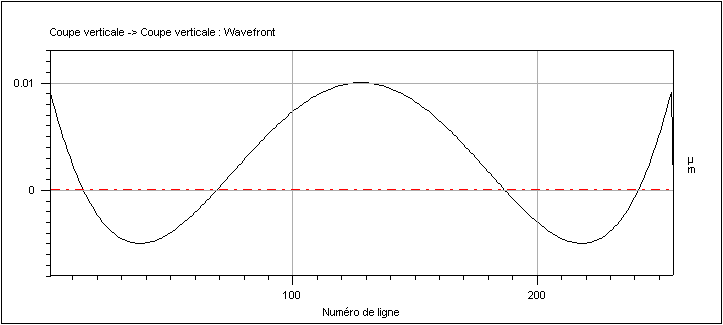Figure 5 : Coupe du front d'onde Lambda/34 P-P

Ecart min (Pixels)

Ecart max (Pixels)

Ecart Rms (onde)

Ecart Peak-Peak (onde) et effet sur la tache d'Airy

-0.05

0.04

Lambda/112

Lambda/34

-0.1

0.09

Lambda/56

Lambda/17

-0.21

0.26

Lambda/22

Lambda/6 (le troisième anneau de diffraction est renforcé, le Sthrel ratio est de 92%)

-0.49

0.5

Lambda/12

Lambda/3.4 (le second anneau est renforcé, Sthrel ratio est de 73%)

Aucune altération n'est visible a Lambda/17, ce qui est une déviation de 0.1 pixels, ce qui très facilement mesurable dans ces conditions par n'importe quel logiciel.

La figure 6 montre la position des spots lorsqu'une onde très formée (25 Lambda) traverse le réseau de microlentilles, en rouge les points de référence, en blanc, ceux mesuré. La figure 7 est la forme du front d'onde correspondante. Des points manquent à cause de l'obstruction centrale et des branches de l'araignée très chargées en câbles.

Figure 6 Figure 7

 


Réalisation pratiques

Pour les expériences, il a été pris une webcam TOUCAM pcvc740K avec comme détecteur, le CCD Sony ICX098BQ qui possède des pixels de 5.6µm : c'est un détecteur simple, il permet d'avoir une vue presque instantané du front d'onde à 30i/sec. Un temps de pose de 1/300 sec avec l'étoile Acturus sur un T600 a été utilisé. Le collimateur est un oculaire clavé de 10mm, et la matrice de microlentilles provient du laboratoire d'optique de Paris-Meudon, il fait 22x22 lentilles carrées de 130µm de pas et de 5mm de focale. Celle ci, m'a été cédé par G.Blanchard : la matrice de microlentille est l'élément important dans cette affaire, il n'est pas facile à trouver, ni très répandu. AMUS en Allemagne en réalise sur catalogue ou sur demande. J'ai eu une fois une proposition pour une matrice 30x30 microlentilles, de 148µm de pas et de 1.3mm de focale (c'est trop court hélas) pour 300€

Le collimateur : il fait 10 mm de focale parce qu'il va produire un diamètre de pupille D2 de 10mm divisé par le F/D du télescope, soit 2.7 mm pour un F/D de 3.7 Si l'on divise 2.7 mm par la taille de chaque microlentille, on trouve que la pupille D2 va illuminer 20x20 microlentilles, soit presque 400 microlentilles : c'est un bon échantillonnage du front d'onde et permet de trouver facilement les polynômes de Zernikes d'ordre élevé, donc des aberrations d'ordre élevé. Si on avait un télescope à F/16, le nombre de microlentilles illuminés serait de 5x5 , ce qui est insuffisant pour du test optique ou de collimation, cela peut l'être pour de la mesure de turbulence. Le dimensionnement du Shack-Hartmann (focale du collimateur et taille et nombre de microlentille, et détecteur associé) dépend de l'application et du télescope. On peut néanmoins envisager pour une matrice de microlentille et un CCD donné avoir différentes focales de collimateur pour s'adapter au F/D du télescope cible. Pour continuer sur le chapitre du collimateur, il est nécessaire de parler de sa qualité optique : s'il altère lui même le front d'onde, ce n'est pas la turbulence, ni la qualité optique et la collimation du télescope que l'on va mesurer, mais bien celle du collimateur. Si le collimateur est de mauvaise qualité optique ou si l'alignement du foyer par rapport au collimateur est mauvais, cela devient critique.

Pour se prémunir du second problème, une mécanique soignée et un diaphragme de champ placé au foyer peuvent arranger fortement les choses. Ce diaphragme de champ ne devra pas faire plus de 0.5mm de diamètre (dans le cas du collimateur 10mm clavé), et sera sur l'axe optique CCD, collimateur et matrice de microlentilles. Il ne faut pas oublier que l'on fait une mesure des spots de référence en plaçant au foyer du collimateur un trou de 10µm, et qu'ensuite sur le ciel les mesures des spots se font en différentiel par rapport à cette matrice de spots de référence. Ce qui veut dire que même si les lentilles ne sont pas bien alignées ente elles (par fabrication), même si le collimateur n'est pas parfait, on peut par mesure différentielle (qui est le principe du Shack-Hartmann) réduire grandement la contribution de ces défauts, par rapport a ceux que l'on va mesurer. La clef du problème tiens plutôt à la qualité de fabrication opto-mecanique des divers éléments optiques. La caractérisation indépendante de la matrice de microlentilles et du collimateur, serait la meilleure des solutions. Je n'ai hélas pas le modèle Zemax d'un oculaire clavé de 10 mm …. Mais compte tenu de ce que j'ai pu voir dans la littérature sur les oculaires Plossl et de la réputation des produits, je ne peux qu'être optimiste. Ne pas oublier que l'on produit une pupille de 2.5mm et non de 6mm (pour l'œil).
J'ai réalisé un montage opto mécanique en bois, ce n'est pas l'idéal, et comme les résultats sont prometteurs j'espère pouvoir le faire réaliser en aluminium. Le système est un cube de 50x50x50mm de coté avec un coulant 31.75mm en entrée. Un tel système est vendu par Imagine Optics, le HASO32 standard avec soft à 22.7k€, le mien a pour le moment coûté le même chiffre avec 2-3 zéros de moins ;-) , mais il est certainement moins performant, alors que celui d'Imagine Optics est un instrument professionnel, ne pas oublier le coût du développement logiciel qui n'est pas négligeable dans cette affaire..

Figure 7a
Cette image est le Shack-Hartmann, a droite, une carte de webcam (démontée), le bloc de bois du milieu contient la matrice de microlentilles (sur une plaquette de verre de 17mm), et le collimateur, qui est le corps qui tient les lentilles d'un oculaire clavé lorsqu'on le démonte.

 

Le fait que ce système n'est pas exactement au foyer du télescope, n'est pas un problème non plus, le defocus produit une homothétie radiale de la matrice des spots sur l'image CCD (dans mon cas), il va produire un coefficient pour Z3 (defocus) non nul, mais ce n'est pas un problème, il sera forcé a zéro pour l'analyse. Mais dans le futur j'éviterais tant que possible le défocus, car c'est facile à régler. La figure 8 montre l'effet du defocus sur le motif de spots.

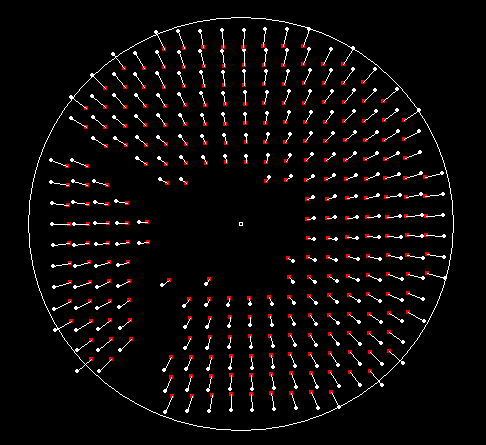Figure 8 Expansion radiale à cause du défocus


Pour l'analyse optique du système, les 600 trames individuelles (20s) de la webcam ont été additionnées. Les effets de la turbulence se moyennent bien, car la turbulence (si elle n'est pas énorme) est une variable aléatoire à moyenne nulle, pour peu que le temps d'acquisition dépasse plusieurs dizaine de secondes, aussi il faut que le tracking du télescope soit correct.
Pour une analyse de la turbulence, on prendra les trames les unes après les autres. Ce type de système permet de faire deux choses : collimation et analyse de l'optique du télescope , et analyse du front d'onde perturbé par la turbulence : c'est pas si mal (!!)
Le Shack-Hartmann a été placé derrière un correcteur de wynne, qui par nature altère quelque peu la tache de diffraction, cependant, je tiens bien à dire que le diaphragme de champ n'était pas a la position optimale du correcteur par rapport a sa dernière lentille, c.a.d 50mm, une position différente altère très vite la qualité optique. Aussi mon montage opto mécanique en bois est très utile pour avoir des images, mais pas pour faire une mesure sûre et définitive. Le but de la manipe n'était pas de caractériser le télescope et son optique, mais d'acquérir des images en vue de réaliser le logiciel, et de valider l'ensemble du concept. Donc les mesures produites ici ne sont en aucun cas définitives et ne sont pas représentatives du système optique. Ceci est un proto. Le jour ou j'aurais un système fait dans les règles de l'art, et non en bois, cela sera possible de le faire, et j'en suis convaincu.

 


Figure 9 : Shack Hartmann test, T600 Valmeca telescope (Acturus, 1/300s a 30i/sec) Somme de 584 images

 


Figure 10 : Shack Hartmann test T600 Valmeca telescope (Acturus, 1/300s a 30i/sec) une des 584 images.

 

Ici la séquence vidéo des 584 trames (impressionnante !) cliquer ici (3.5Mo), il faut DivX Decoder (L'obtenir ici). On voit les spots disparaître (scintillation), et le grouillement dû à la turbulence.

Réduction des données

C'est une partie qui a demandée pas mal de programmation pour la rendre facile et conviviale, il a été intégré dans le logiciel PRISM, la première étape est d'extraire les spots automatiquement et de les classer (Figure 11). Il y a 261 spots.

Figure 11, fichier résultant de l'addition des 584 images

La seconde étape consiste à charger un fichier Ascii contenant la position X et Y des spots de référence (415) trouvé dans l'image de la figure 2a.

Une fois chargé, il faut indiquer à quel spot numéro A de la figure 11 correspond le spot de numéro B de la figure 2b, en plus quelques renseignement sur le système.

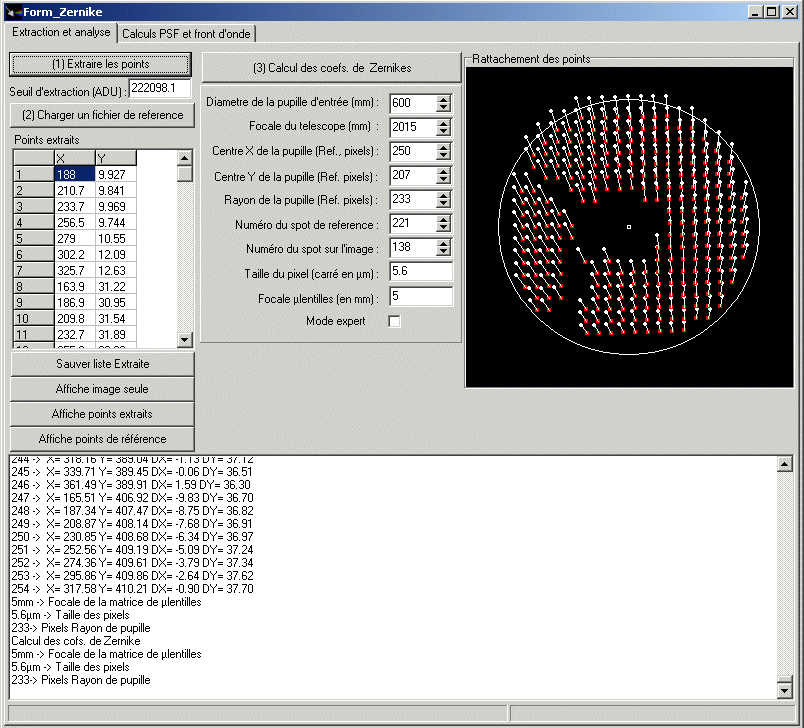Figure 12

Une fois les rattachements des spots entre l'image mesuré et l'image de référence sont trouvé (automatiquement aussi), on peut calculer les écarts de position et donc les polynômes de Zernike. Le décalage en X et en Y de l'ensemble des spots entre l'image mesuré et la référence n'est pas important, car il produit les termes Z1 et Z2, qui n'est qu'un décalage global de l'image pas une aberration

Le panel de la figure 13 montre les coefficients a1....a19 des polynômes de Zernikes. Les coefficients de Tilts et de defocus sont mis a zéro, car ils ne représentent pas en soit des défauts optiques.

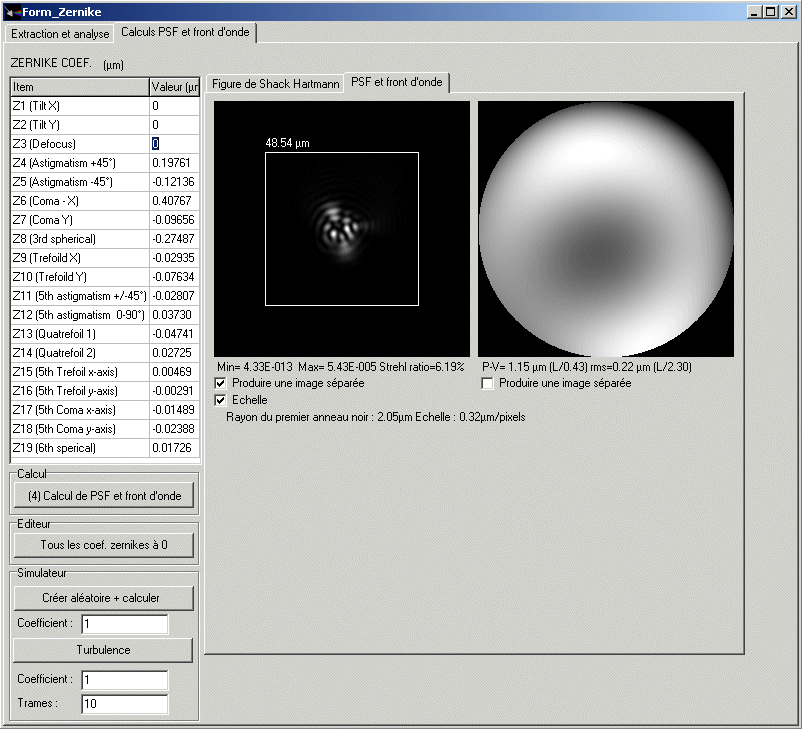Figure 13

Une fois les coefficients de Zernike trouvés, on peut à loisir les modifier et regarder quelle est la tache image correspondante (PSF). Plus le coefficient Zn est fort, plus l'aberration sera visible sur l'image. Comme le front d'onde est connu, le calcul de la PSF est possible : ce ne sont que des mathématiques.


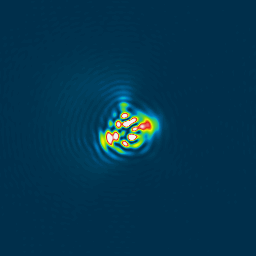
Figure 14a, b et c , de gauche à droite, PSF (ou image) de l'étoile.

La figure 14a, et ce que l'on appelle la PSF d'une étoile (la turbulence a été minimisée par l'addition des 584 images), la figure 15 est la PSFpour un système parfait. Si on mets à zéro le terme de coma (Z6 et Z7), on voit sur la figure 14b l'amélioration, si on met à zéro les termes Z4 et Z5 d'astigmatisme, on obtient la figure 14c, qui semble être entachée d'aberration de sphéricité (ce qui est un peu normal après un correcteur de champ). Vous allez dire que je triche, certes, mais il est intéressant de voir l'impact de chaque aberration sur les images : j'aurais un barillet qui induit une déformation sur le miroir primaire, je la mesure, et je peux mettre la contribution à zéro du barillet en mettant a zéro le bon coefficient de Zernike, et décider, au vu du résultat, si ça vaut le coup de refaire le barillet.........

Figure 15 PSF parfaite, à la même échelle, l'image fait 0.32µm par pixel au foyer du T600 a F/3.7

Effets de la turbulence

Et la turbulence ? Si on calcule des motifs de spot sur des images individuelles de la séquence de 584, on remarque que les PSF sont fort différentes les unes des autres...


Figure 15 a,b et c : trames 472, 524 et 532

Ce qui milite pour dire que l'on a intérêt à additionner un maximum d'images pour ne pas être gêné par la turbulence.... une séquence de 2min ne serait pas de trop.


Figure 16 a et b, trames 470 et 469

La figure 16 montre deux trames consécutives, à 33ms d'intervalle : il est évident que les PSF sont trés differentes

Amélioration possibles

Tout ça s'annonce prometteur, mais il y a des axes de progrès à dégager :

A faire, une fois les améliorations réalises :
- des tests sur un télescope dont l'optique est caractérisée à 100% par un autre système (Zygo ou Foucault à la rigueur)

Questions

Cette page fait référence à des questions réponses sur ce système.

D'autres liens

Une réalisation faite avec un industriel


Références

Des articles qui m'ont bien aidé à avancer .......

  1. Tout savoir sur la théorie des aberrations et des polynômes de Zernikes
  2. An Interferometric Hartmann Wavefront Analyzer for the 6.5m MMT, and the First Results for Collimation and Figure Correction
  3. Interferometric Hartmann wave-front sensing for active optics at the 6.5-m conversion of the Multiple Mirror Telescope

Et merci à G.Blanchard, S.Guisard, A Maury et S.Deconhiout pour la lecture du texte et pour l'aide apportée

par Cyril Cavadore (Mai 2003), retour à la Home Page