There are six different versions of VSOP87 :
The main version (VSOP87) permits to compute the elliptical elements.
Versions A and C give heliocentric cartesian (rectangular) coordinates ;
Versions B and D give heliocentric spherical coordinates ;
Version E gives barycentric catresian coordinates ;
For all the versions, time argument is TDB, and reference frame is BRS.
Our purpose is to compute :
- heliocentric geometrical and apparent coordinates, and
- geocentric apparent equatorial and ecliptic coordinates.
So we'll have to perform coordinate transformations ; it's then simpler to work with cartesian coordinates and transform to spherical just before displaying the results. Versions A and C are then appropriate.
For version A, the reference frame is defined by the dynamical equinox and ecliptic J2000.
For version C, the reference frame is defined by the dynamical equinox and ecliptic of the date.
|
(see farther for details about frames) |
Precession has been applied to go from the frame of version A to the frame of version C. I first thought that using version C would permit to avoid precession computation. We'll see farther that it's not possible (because matrix multiplication is not commutative).
So we'll use version A (version D is used in XEphem, and version A in WinAstro).
In BDL server, we find one file per planet. Here is an extract of VSOP87 file (for Neptune, version A) :
VSOP87 VERSION A1 NEPTUNE VARIABLE 1 (XYZ) *T**0 772 TERMS HELIOCENTRIC DYNAMICAL ECLIPTIC AND EQUINOX J2000
1810 1 0 0 0 0 0 0 0 1 0 0 0 0 -0.00682678287 30.05889926953 30.05890004476 5.31211340029 38.13303563780
1810 2 0 0 0 0 0 0 0 0 0 0 0 0 0.00000000000 -0.27080164222 0.27080164222 3.14159265359 0.00000000000
etc...
1810 771 0 0 0 0 6-16 0 2 0 0 0 0 0.00000001037 -0.00000001976 0.00000002232 2.42169508541 158.37366516480
1810 772 0 0 0 0 0 0 19-20 0 0 0 0 0.00000000619 0.00000002392 0.00000002471 3.93681150847 658.18966002270
VSOP87 VERSION A1 NEPTUNE VARIABLE 1 (XYZ) *T**2 102 TERMS HELIOCENTRIC DYNAMICAL ECLIPTIC AND EQUINOX J2000
1812 1 0 0 0 0 0 0 0 0 0 0 0 0 0.00000000000 0.00005371138 0.00005371138 0.00000000000 0.00000000000
1812 2 0 0 0 0 0 0 1 -1 0 0 0 0 0.00004488541 0.00000656405 0.00004536283 5.02700751836 36.64856292950
etc...
1812 101 0 0 0 0 1 0 0 -1 0 0 0 0 0.00000001759 -0.00000001439 0.00000002273 5.59760233612 491.55792945680
1812 102 0 0 0 0 0 3 0 -4 0 0 0 0 -0.00000002773 -0.00000000305 0.00000002790 1.90430778774 487.36514376280
etc..
From VSOP87.doc, we can find out that coordinates can be computed in two different way ; the simplest way uses only the three last numbers of each row (called A, B, C).
The formula to use is :
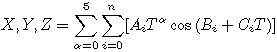
Derivating with respect to time, we get the velocities :
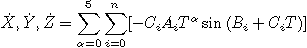
Where :
- Ai, Bi, Ci are the terms in the BDL file.
- n is the number of terms given for a planet and a power of time (for example, n = 772 for Neptune, for variable X, T 0).
- T is in thousands of julian day from JD2000, T = (jd - JD2000) / 365250 (see the page dealing about time for more details).
To compute the coordinates, we need :
a class which computes the summation : done by jephem.astro.solarsystem.vsop87.VSOP87 ;
files to store the data.
As we only need the terms Ai, Bi, Ci, the first thing to do is to remove the other terms from the original files. This has been done by a class which is not part of JEphem package : BuildVSOP87.java (you can get it from download area - use of BuildVSOP87.java is described in its javadoc page). BuildVSOP87.java permits to generate files containing terms Ai, Bi, Ci in 3 different formats : raw text; formatted java class, and binary format.
Full precision version
The ideal would be to format the data into java classes (a double[][][] array), and compile the classes. This would permit to keep the data in binary format, and let the data usable by applets (which can't read files). But a specification of JVMs (Java Virtual Machines) imposes a limit : the size of a compiled class must not exceed 64 Ko.
So I used binary format to store the values, generating one file per planet. At execution time, the data are retrieved from the files. The class which performs the computation (jephem.astro.solarsystem.vsop87.VSOP87) stores the data in static variables, so file reading is done only at first computation.
In JEphem hierarchy, the data files are stored in directory Jephem/data/astro/planets/vsop87/VSOP87A (see page 'JEphem directories' of informatic trail for details). The files are named DataVSOP87A_Full_Xxx (where 'Xxx' stands for the name of a planet).
Truncated version
Having lower precision routines is interesting when large amounts of computations need to be done.
So a question arises : how to truncate the series in order to keep only the terms useful to get a given precision? An answer is given in A&A 202 p 314 : they say it's possible to have a precision of 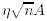 , where :
, where :
- h is a number smaller than 2 (XEphem uses 2) ;
- n is the number of terms retained ;
- A is the amplitude of the smallest term retained retained.
I first found this formula in XEphem comments, but I didn't know if this could be applied to cartesian coordinates. I found the A&A article later. So I tried to answer to the question. This is detailed in the next page, Truncating VSOP87.
As we'll see in Testing VSOP87, there is an error in my home made truncation : I wanted a precision of 1 arc second, and got a precision of 4 arc seconds. For the moment, I kept this version, because I couldn't get coherent results from the formula found in A&A.
This time, it was possible to generate java classes which don't exceed 64 Ko. BuildVSOP87.java was also used to generate them. The generated classes are jephem.astro.solarsystem.vsop87.DataVSOP87A_JEphem_Xxx (Xxx designate a planet name) ; the suffix "_JEphem" indicates that the class was generated using JEphem truncation method.
I made tests to compare execution time using these java classes and binary files of the truncated version. It appeared to be equivalent. So I kept the java classes for the truncated version, as they can be used by applets.
Computing the summation
The class which performs the summation is jephem.astro.solarsystem.vsop87.VSOP87 ; the method to call is calcCoord().
I wrote VSOP87.java from the fortran code found in example.f in BDL's FTP site (XEphem code was also useful to undersand the fortran code).
This did not present major difficulties.
There is still a point that I did not understand : how precision control works (variables prec, p, q in the code). The routine is called with a parameter, precision. During the summation, a test is done to know if a given term should be taken into account. This is the test I did not understand.
VSOP87.calcCoord() takes a parameter, precision. For the moment, if precision < 4 arc seconds, full version is used, otherwise truncated version.
Computation time
Here is the time taken to compute one planetary position ; (average time taken on 100000 computations for Mercury).
| Full | Truncated |
Average computation time
(PC 1,6 GHz, 256Mo RAM) | 3.4 ms | 0.09 ms |
Computation is 38 times faster for the truncated version.
Size
| Full | Truncated |
| Total size (Binary format) | 923 Ko | 70 Ko |
Number of terms
|
VSOP87A_Full
(BDL) | VSOP87A
(JEphem) | VSOP87D
(XEphem) |
| Mercury | 6359 | 135 | 277 |
|
| Venus | 2357 | 378 | 169 |
|
| Earth | 3538 | 234 | 406 |
|
| Mars | 7073 | 793 | 691 |
|
| Jupiter | 4434 | 360 | 1056 |
|
| Saturn | 7512 | 449 | 1833 |
|
| Uranus | 5289 | 458 | 1380 |
|
| Neptune | 2636 | 123 | 563 |
|
| Total | 39198 | 2930 | 6375 |
| |



 Ephemeris trail
Ephemeris trail
 Building VSOP87
Building VSOP87



 Ephemeris trail
Ephemeris trail
 Building VSOP87
Building VSOP87
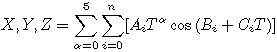
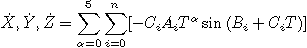
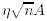 , where :
, where :