Pluto99

Pluto99 Characteristics Building and testing positions Obtaining the velocities Testing velocities Remarks

I couldn't find the official name of the theory I used to compute Pluto ephemeris, so I called it "Pluto99", as it has been released in 1999.
The theory is from Jean Chapront and Gérard Francou from the "Observatoire de Paris" (Paris Observatory).
The original files can be found at ftp://ftp.bdl.fr/pub/polac/solarsys/pluto. Files plutoxyz.dat, plutoxyz.for and notice have been used.
The resulting class to compute Pluto coordinates is jephem.astro.solarsystem.Pluto99. See its javadoc page for more information.

Pluto99 characteristics

Here are some extracts of BDL files :

Tables of Pluto's motion have been constructed by the first author using
a method of approximation based on frequency analysis as described in the
paper :
Representation of planetary ephemerides by frequency analysis.
Application to the five outer planets.
Astron. & Astrophys.Suppl. Ser., 109, 191 (1995).

This representation uses the results of the numerical integration DE406
of the Jet Propulsion Laboratory as a source.

The interval of validity covers 2185000 days (60 centuries approximately).
Start : Apr 23 -2998 0h, Julian date  626150.5
End   : Jul 26  2984 0h, Julian date 2811150.5

The reference frame is defined with dynamical equinox and ecliptic J2000.
The time scale is Barycentric Dynamical Time (TDB).

The largest discrepancy obtained by a comparison with the source DE406
is 0.00005 ua.

Precision of the theory in arc seconds :
The worst case happens when distance Sun - Pluto is minimal and when the Earth is between the Sun and Pluto.
The value of Pluto perihelion is 29.65 a.u. So the minimal distance between the Earth and Pluto is 28.65 a.u.
So an error of 0.00005 a.u. corresponds to arctan(0.00005/28.65) radians.
This corresponds to 0.36 arc seconds.

Building and testing positions

The class used to build and test Pluto99.java is BuilTestPluto99 (see its javadoc or code source).

Here is what has been done :

Building data file : I transformed the original plutoxyz.dat with BuildTestPluto99.buildPluto99(). In notice, thet say that "The largest discrepancy obtained by a comparison with the source DE406 is 0.00005 ua" ; seen from Earth, this corresponds to a maximal error of 0.37 arc second (for a geocentric opposition Sun - Pluto, when distance from Pluto to Sun was minimal - see BuilTestPluto99.calcGeoPrec()). I thought it was no use to build a light version giving a precision of one arc second.
As there are "only" 659 terms (corresponding to 32.5 Ko in ASCII format), it was no use putting the data in a separate file. So the transformation of the original file was just a matter of formatting the terms in java-formated arrays. During formatting, I removed term called 'Period' as it's not used in the computation.

Writing Pluto99.java : I included the previously built arrays in Pluto99.java with cut'n'paste. I then wrote the method to perform the computation (Pluto99.calcCoord()), from the informations found in notice. As it's straightforward, I don't detail this here.

Testing : I then tested the routine with BuildTestPluto99.testPositions(). The differences between reference values from the BDL and JEphem values are about 10^-7 u.a., which is OK, as the announced precision is 10^-5 u.a.

Building a new version : in the original file, the term 'Phi' is expressed in degrees, and must be converted in radians during the computation. This represents 659 operations that can be avoided if the terms are directly expressed in radians.
So with buildPluto99(), I generated an other class with values in radians.

Testing again : term 'Phi' is given with a precision of 10^-5 degree, which corresponds to 1.75*10^-7 rad. A priori, 7 digits for the terms expressed in radians should be enough, but I was not sure : errors may accumulate and lead to lower precision. The same tests as above done with the radian version also gave me differences of 10^-7 u.a. So it was OK for the positions.

Obtaining the velocities

In BDL's original files, they only give a formula for the positions. And I also wanted to have the velocities.
The situation is similar to VSOP87 : positions are obtained by a summation of terms, and each term is a function of time.

In VSOP87, to obtain the formula of velocities, they simply derivate the formula giving a term for position, and the velocity is a summation using the obtained formula.
So I did the same for Pluto99. I hope it's correct ; tests (see below) seem to indicate that the values are coherent, but I have NOT matched these velocities with reference values.

Using the notations of notice, we have (for X, Y, Z) :

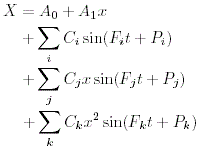(formula 1)

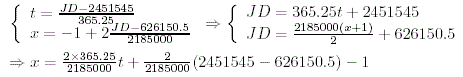
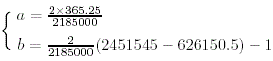
Before derivating, we need to express the x in function of t. We have :

If we note :

We have :

x = a*t + b

Formula 1 then becomes :

Derivating this formula, one obtains :

X, Y, Z are expressed in a.u ; t is expressed in Julian years. So we should get the velocities in a.u. per Julian year. If we want them in Julian days, we sould simply divide the result by 365.25

Testing velocities

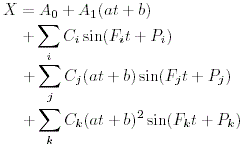
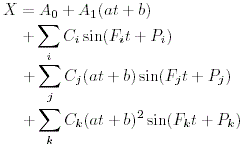
To test the velocities, I wrote a method (BuildTestPluto99.testVelocities()). To test the velocity at instant t, it computes the position at t - dt and t + dt, computes the average velocity and compares it to the value obtained with the preceding formula at instant t.
I tested with dt = 1 day and dt = 0.1 day, and had differences of 10^-10 (a.u. per year).

So I considered that the velocities were OK.

Remarks

The parameter 'precision' of Pluto99.calcCoord() is NOT used ; all the terms are taken for the summation.

JEphem Presentation Ephemeris SkyMap Curve Informatic Library Download Glossary About
	JEphem Ephemeris trail Pluto 99