In [BDL98], p. 89, they say that the coordinates given by the theories (VSOP87, ELP82, and I suppose Pluto99) are expressed in a Barycentric Reference System (BRS) (I couldn't find this information in BDL's FTP files).
Usual coordinates are expressed in a reference frame called FK5. Reference frame stuff seems complex : they talk about "inertial ecliptic", "rotational ecliptic" ... but apparently, it's possible to skip these notions ; the only important thing is to transform the coordinates to get to the FK5. Fortunately, they indicate how to do this in the BDL's FTP files.
In VSOP87 and Pluto99, they say that "the reference frame is defined with dynamical equinox and ecliptic J2000". Both give heliocentric ecliptic coordinates. So the same treatment can be applied in both cases. The case of the moon is handled separately (ELP gives coordinates in a different frame).
Planetary theories give geometric heliocentric ecliptic coordinates.
The first step is to take into account an effect called light aberration :
|
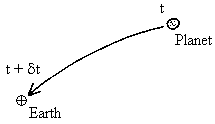
Imagine that someone on a planet sends a signal at instant t.
On Earth, we'll recieve the signal at instant t + dt (dT is the time taken by light to go from planet to Earth).
So at instant t on Earth, we see the planet at its position at instant t - dt.
So if we want to have the apparent coordinates of the planet at instant t on Earth, we must calculate them at instant t - dt.
|
To handle this, we must :
Compute the position of the Earth at instant t;
And for each planet :
Compute positions at instant t ;
Calculate dt (we have : dT = EP/c (c = light speed));
Compute coordinates of the planet at instant t - dt.
This means that the coordinates of the planet must be calculated twice.
Note : in some cases, the planetary theories (like VSOP87) give us the velocities. This could be used to save up the second computation :
we have : v = dx/dt ; this is the limit of dx/dt, when dt nears 0. If dt is small, we could approximate and say : v = dx/dt, and get dx from this whithout computing a second time.
I haven't tested in which cases this method could give interesting results (with enough precision), but should try one of these days.
In heliocentric frame, we have the coordinates of all the planets including the Earth.
In geocentric frame, we'll have the coordinates of the Sun, obtained from the heliocentric coordinates of the Earth.
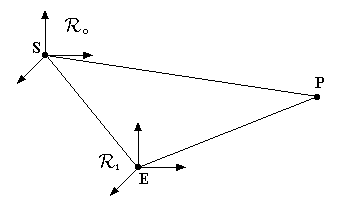 |
R0 : heliocentric frame
R1 : geocentric frame
E : Earth
P : planet
S :Sun |
For the planets
We know coordinates of P and E in frame R0, and we want to know the coordinates of P in R1.
We note : 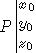 and
and 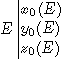 the coordinates of P and E in R0 ;
the coordinates of P and E in R0 ;
and 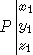 the coordinates of P in R1.
the coordinates of P in R1.
The purpose is to find x1, y1, z1 from x0, y0, z0.
We have :
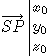 ,
, 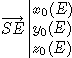 and
and 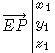
And :
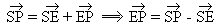
Then : 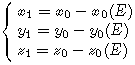
For the Sun and the Earth
The coordinates of the Earth in R0 are the coordinates of 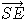 ; the coordinates of the Sun in R1 are the coordinates of
; the coordinates of the Sun in R1 are the coordinates of 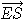 ;
;
If we note 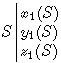 the coordinates of S in R1 :
the coordinates of S in R1 :
As 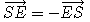 , we have :
, we have :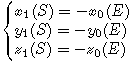
Case of the velocities
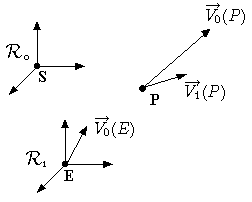 |
R0 : heliocentric frame
R1 : geocentric frame
E : Earth
P : planet
S :Sun
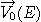 : velocity of Earth in R0 : velocity of Earth in R0
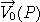 : velocity of planet in R0 : velocity of planet in R0
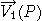 : velocity of planet in R1 : velocity of planet in R1
|
We know 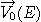 and
and
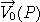 and we want to know
and we want to know
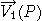 .
.
We simply have :
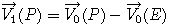
For the Sun and the Earth : 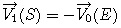 To agree with each other, astronomers (through the IAU - International Astronomical Union) define frames in which usual coordinates should be expressed.
To agree with each other, astronomers (through the IAU - International Astronomical Union) define frames in which usual coordinates should be expressed.
The current frame is the ICRF (International Celestial Reference Frame), adopted in 1998.
The previous frame was FK5, built in 1988 from measures of positions of 1535 stars. [I read that the name "FK5" comes from "Fundamental Katalog" and that the name "FK4" (in use before the FK5) comes from "Fricke and Kroppf", the persons who built the FK4 in 1963].
For the moment, the coordinates of JEphem are expressed in the FK5 (as it was easier), but I hope to change this in the future.
In vsop87.doc, they give the rotation matrix to connect the coordinates given by VSOP87A with the "equatorial frame FK5 J2000".
WARNING : in [
BDL98], p. 90, they give this matrix,
which is different from the one given in vsop87.doc. The 3 last digits are different. In JEphem, I used the values of vsop87.doc (the only reason is that I could do copy'n'paste...).
But this is a question to solve.
We must now take into account the movements of the Earth's axis of rotation : precession and nutation, and understand the meaning of "mean" and "true" coordinates. This is defined in p. 104 of [BDL98] :
| Coordinate | Reference plane | Origin |
|---|
| Mean ecliptic of a reference date (ex : J2000) |
Mean ecliptic of the reference date |
Mean equinox of the reference date |
| Mean ecliptic of a date |
Mean ecliptic of the date |
Mean equinox of the date |
| True ecliptic |
Mean ecliptic of the date |
True equinox of the date |
| Mean equatorial of a reference date |
Mean celestial equator of the reference date |
Mean equinox of the reference date |
| Mean equatorial of a date |
Mean celestial equator of the date |
Mean equinox of the date |
| True equatorial |
True celestial equator of the date |
True equinox of the date |
In p. 80 of [BDL98], they give the following definitions :
The true equator of a date is the plane perpendicular to direction of the celestial pole.
The mean equator of a date is deduced from the true equator of the date by a transformation given by the nutation theory.
Mean Ecliptic can be inertial or rotational, and have a cinetic definition.
The following definition is not used (but interesting, so I also copied it).
True ecliptic is defined as the osculating plane of the heliocentric movement of the Earth-Moon barycenter. It is never used as a reference plane.
The true equinox of a date is the ascending node of the mean ecliptic on the true equator at this date.
The mean equinox of a date is the ascending node of the mean ecliptic on the mean equator at this date.
Mean ecliptic and Mean Equator of a given date are fix planes that can be used as a reference plane
These definitions are used to transform mean coordinate given by the theories to true coordinates, commonly used.
in a first step, precession and nutation are not taken into account. This permits to have a fix reference plane (Eq or Ec - for example Mean Equator of J2000) ; the origin is the mean equinox. The coordinates are the mean coordinates of the reference date.
Then precession is applied, and the reference plane is the mean plane of the date, the origin is the mean equinox of the date. The coordinates are the mean coordinates (Eq or Ec) of the date.
Then nutation is applied, and the origin is the true equinox of the date. The reference plane is the True Equator or the Mean Ecliptic of the date ; the coordinates are the true coordinates of the date.
Question : What do we call the Vernal Point ?
A priori, this is the true equinox of the date, intersection of :
- mean Ecliptic of date, and
- true equator of date
So to get the real direction of the vernal point ("true vernal point" ?), should we compute the position of true Ecliptic ? Are there works available somewhere to do that ? Does this make sense ?
Notations used in the following paragraphs (from [BDL98], p. 103) :
Equatorial cartesian coordinates are noted xA, yA, zA.
Ecliptic cartesian coordinates are noted xE, yE, zE.
The transformation described in the To FK5 paragraph permited to get the mean geocentric equatorial coordinates J2000.
Now to get the mean geocentric equatorial coordinates of date, the precession must be applied to the coordinates.
To compute precession, I once again used
a BDL's theory : prcbdl94, which can be found at ftp://ftp.bdl.fr/pub/ephem/ref-frames/prcbld94 ;
The explanations of chapters 4.5 and 5 of [BDL98] ;
The article "Numerical expressions for precession formulae and mean elements for the Moon and the planets" from Astron. Astrophys. 282, 663 (1994).
In [BDL98] p. 106, they give a formula which permits to get the coordinates  , refered to the mean equator of a date sD, from the the coordinates
, refered to the mean equator of a date sD, from the the coordinates 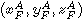 , refered to the mean equator of a date sF (I guess that F stands for Fixed and D for Date).
, refered to the mean equator of a date sF (I guess that F stands for Fixed and D for Date).
This transformation is :
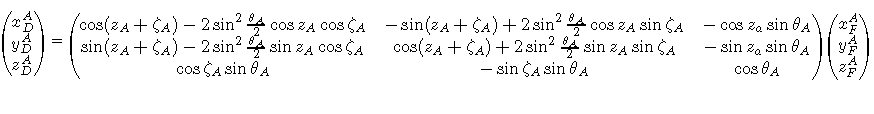
The 3 variables qA, zA, zA can be computed with prcbdl94, from t and T.
In prcbdl94, they introduce an other epoch, s0 (the base epoch, J2000), and define two other variables :
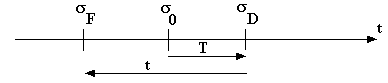 |
T = sF - s0
t = sD - sF
|
I have not understood the necessity to introduce s0.
Anyway, here, we don't need it, because the "departure date", sF is J2000, and the base epoch s0 is also J2000. So sF = s0, then T = 0.
It is then possible to implement simplified formulae.
WARNING : the formulae of prcbdl94 (in file prctable.doc) are also given in [
BDL98] p. 131, and in the A&A article (formulae 6, p. 665) ; A&A and prcbdl94 formulae seem to be identic (I didn't check all the terms), but some terms of formulae given in [
BDL98] differ, and I don't know why. For JEphem, I kept prcbdl94 formulae (with copy'n'paste).
The formulae use constants defined by UAI in 1976 ; complementary formulae are given to take into account the new values of 1992. I could'nt understand this neither from [BDL98] nor from BDL's FTP files. I finally got it from the A&A article.
For the complementary terms, I used formulae 8 p. 667 of the A&A article.
I copied here an extract of the A&A article, as it may be useful for the future.
ZZZZ
Put here extract
ZZZZ
Implementation and tests
The computation of qA, zA and zA is handled by jephem.astro.MeanTrue.
For the precession variables, I first implemented the formulae of prctable.doc (I implemented all the formulae, even if some are useless for the moment).
I tested to match the values given at the end of prctable.doc (The test methods are at the end of MeanTrue source code).
I asked a computation with sF = J2000, wrote the simplified formulae (when T=0), and checked that the simplified formulae give the same result as full formulae.
I then included the complentary formulae.
Warning
- I had no values to test the complementary formulae.
- I don't know if it's a good idea to have precession computed with 1992 IERS values of planet masses as VSOP87 is built with 1976 UAI values.
MeanTrue is not a static class ; an instance of MeanTrue is holding the precession variables.
Finally, the public methods of MeanTrue are just getQuantity() and getEqPrecessionMatrix() (see MeanTrue javadoc).
The previous paragraph permitted to compute the mean geocentric equatorial coordinates of date.
The purpose is now to get the true geocentric equatorial coordinates of date, applying nutation to coordinates.
This transformation can be found in [BDL98] p.109 :
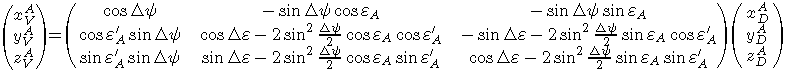
where 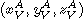 are the coordinates we are looking for, refering to the true equator.
are the coordinates we are looking for, refering to the true equator.
eA can be calculated from prcbdl94 ;
e'A = eA + De ;
the computation of Dy and De involves a summation of 106 terms, described p.138 of [BDL98] ; the terms are : Ai, A'i, Bi, B'i, and six terms named "ARGUMENT" : l, l', F, D, W.
The formulae given in [BDL98] are :
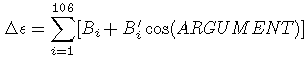 and
and
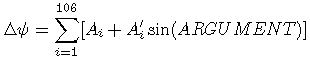
I couldn't find in [BDL98] what sin or cos(ARGUMENT) could mean. Fortunately, a friend told me (merci Alain) : each of the 6 variables of ARGUMENT must be multiplied by the corresponding Delaunay argument. I found the expressions of Delaunay arguments in the same A&A 282 article, p. 670.
Finally, I needed an electronic version of the terms to sum. I took it from XEphem code (nutation.c).
Implementation and tests
I wrote an other class to handle the summation of terms : jephem.astro.Nutation. This is a static class, which is written as an auxiliary class of MeanTrue ; this class just has one public method : getDeltaPsiEpsilon.
An other method was written in class MeanTrue : getEqNutationMatrix() - see MeanTrue javadoc.
Warning : I did not test nutation.
Getting true ecliptic coordinates 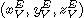 is quite straightforward : keeping the same notations, the transformation is :
is quite straightforward : keeping the same notations, the transformation is : 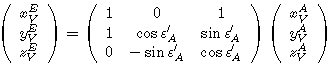 (cf [BDL98], p. 103).
(cf [BDL98], p. 103).
This matrix is returned by MeanTrue.getTrueEqToEcMatrix()
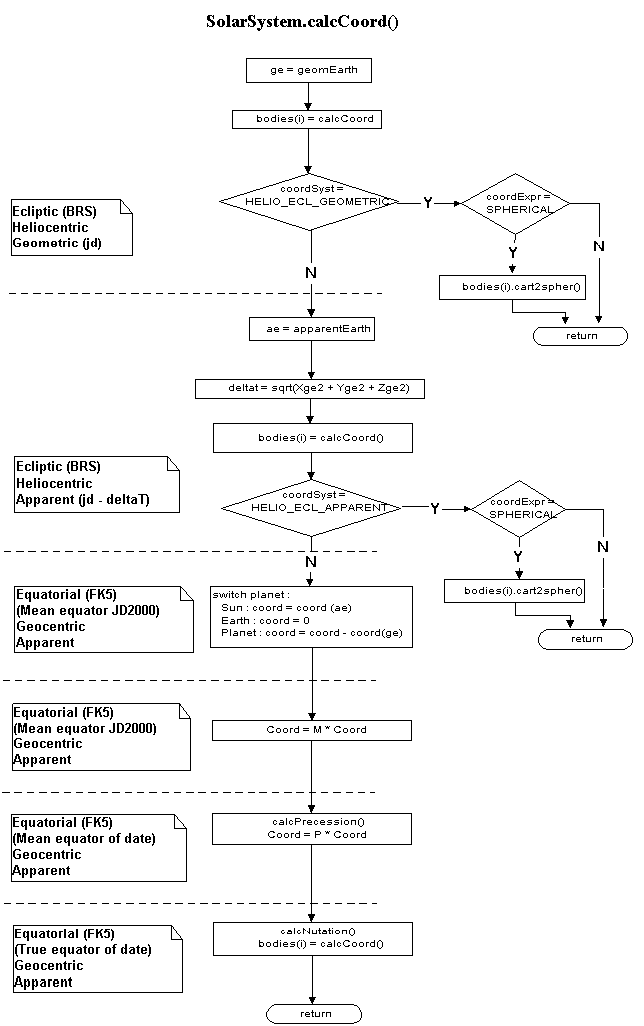
The following flowchart summarizes the transformations done in SolarSystem.java.
The purpose was to be able to retrieve coordinates expressed in different frames ; so SolarSystem.calcCoord() takes a parameter coordExpr.



 Ephemeris trail
Ephemeris trail
 Coordinate transformations
Coordinate transformations



 Ephemeris trail
Ephemeris trail
 Coordinate transformations
Coordinate transformations


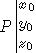 and
and 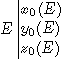 the coordinates of P and E in R0 ;
the coordinates of P and E in R0 ;
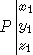 the coordinates of P in R1.
the coordinates of P in R1.
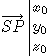 ,
, 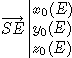 and
and 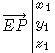
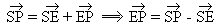
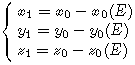
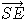 ; the coordinates of the Sun in R1 are the coordinates of
; the coordinates of the Sun in R1 are the coordinates of 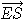 ;
;
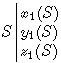 the coordinates of S in R1 :
the coordinates of S in R1 :
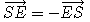 , we have :
, we have :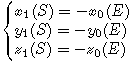

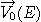 : velocity of Earth in R0
: velocity of Earth in R0
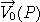 : velocity of planet in R0
: velocity of planet in R0
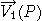 : velocity of planet in R1
: velocity of planet in R1
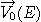 and
and
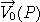 and we want to know
and we want to know
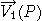 .
.
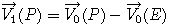
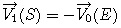
 , refered to the mean equator of a date sD, from the the coordinates
, refered to the mean equator of a date sD, from the the coordinates 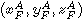 , refered to the mean equator of a date sF (I guess that F stands for Fixed and D for Date).
, refered to the mean equator of a date sF (I guess that F stands for Fixed and D for Date).
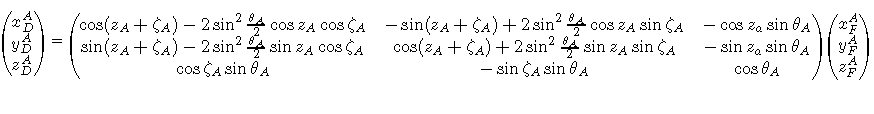
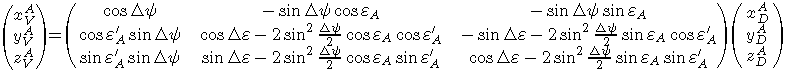
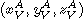 are the coordinates we are looking for, refering to the true equator.
are the coordinates we are looking for, refering to the true equator.
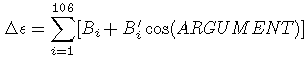 and
and
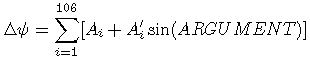
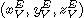 is quite straightforward : keeping the same notations, the transformation is :
is quite straightforward : keeping the same notations, the transformation is : 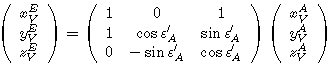 (cf [BDL98], p. 103).
(cf [BDL98], p. 103).