Les polynômes de Zernike

Les Polynomes de Zernike

Les polynômes de Zernike sont des fonctions de deux variables (x et y en coordonnées cartésiennes) définies sur le disque de rayon unité. Ces fonctions permettent de modéliser un front d'onde lorsqu'elles sont Combinées linéairement entre elles, c'est à dire lorsque chaque fonction est multipliée par un coefficient (dit coefficient de Zernike) puis les résultats additionnés.

Les 22 polynomes (ou modes) du tableau 1 sont trés utilisés dans la pratique pour reconstituer les fronts d'onde. La figure 1 montre les conventions utilisées ici. Attention, il existe beaucoup d'autres conventions !

Les polynômes de Zernike présentent plusieurs propriétés remarquables. Nous décrivons ici brièvement celles qui sont utiles à l'opticien. (Pour plus de détails consulter les pages spécialisées).

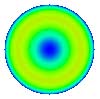
Les premiers modes peuvent être relié aux principales aberrations. par exemple W₁₁ décrit l'aberration dite de sphéricité (aberration de sphéricité du troisième ordre). On reconnait sur la représentation graphique la forme caractéristique de cette aberration : une "bosse" au centre et un bord relevé (en bleu). Remarque : il s'agit ici de la sous-correction de sphéricité. Pour décrire la surcorrection, il suffit de multiplier W₁₁ par un coefficient négatif.
L'écart RMS de chaque polynôme est égal à l'unité. Ainsi, chaque coefficient de Zernike est égal à la valeur RMS de l'aberration correspondante. Par exemple, si un front d'onde est entaché de l'aberration de sphéricité, il peut être représenté par le polynôme W₁₁ multiplié par un coefficient z₁₁. La valeur de ce coefficient donne la valeur RMS de l'aberration de sphéricité.

W(x,y)

A B C

Fig.1 : Conventions utilisées ici pour la représentation des polynômes de Zernike : (A) Cercle de rayon unité. (B) Systèmes de coordonnées cartésiennes et polaires (C) Palette de couleurs utilisée pour la représentation du front d'onde.

n du mode et aberration correspondante Expression de W_n(x,y) Représentation

1. Piston 1

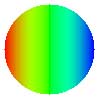
2. Inclinaison du front d'onde selon x (x tilt) x

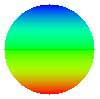
3. Inclinaison selon y (y tilt) y

4. Défocalisation (defocus) 2r²-1

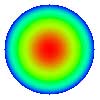
5. Astigmatisme à 0° x²-y²

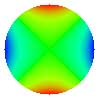
6. Astigmatisme à 45° 2xy

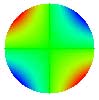
7. Coma selon x (3r²-2)x

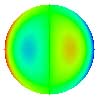
8. Coma selon y (3r²-2)y

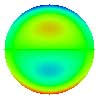
9. Trefoil (x²-3y²)x

10. Trefoil (3x²-y²)y

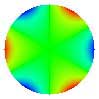
11. Sphéricité 6r⁴-6r²+1

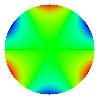
12. Astigmatisme secondaire 4(x⁴-y⁴)-3(x²-y²)

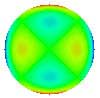
13. Astigmatisme secondaire (8r²-6)xy

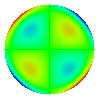
14. Tetrafoil x⁴+y⁴-6x²y²

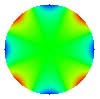
15. Tetrafoil 4(x²-y²)xy

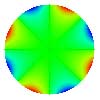
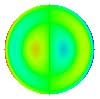
16 Coma secondaire (10r⁴-12r²+3)x

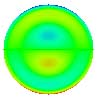
17 Coma secondaire (10r⁴-12r²+3)y

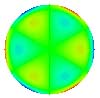
18 Trefoil secondaire (5x⁴-10x²y²-15y⁴-4x²+12y²)x

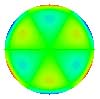
19 Trefoil secondaire (15x⁴+10x²y²-5y⁴-12x²+4y²)y

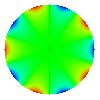
20 Hexafoil (x⁴-10x²y²+5y⁴)x

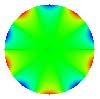
21 Hexafoil (5x⁴-10x²y²+y⁴)y

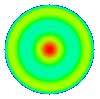
22. Sphéricité secondaire (6° ordre) 20r⁶-30r⁴+12r²-1

Tab. 1 : Polynômes de zernike et principales aberrations.
On remarque les propriétés de symétrie. Les polynômes W₁, W₄, W₁₁ et W₂₂ sont invariants par rotation (symétrie de révolution : leurs expressions ne dépendent que de r). Les autres polynômes présentent au moins un axe de symétrie et sont présents en deux "exemplaires" tournés l'un par rapport à l'autre d'un angle de 90° divisé par le nombre d'axes de symétries. Par exemple, W₅ et W₆ (astigmatisme) présentent deux axes de symétrie et sont tournées l'un par rapport à l'autre de 45°. Cette propriété de symétrie permet de reproduire, par combinaison linéaire des deux polynômes W₅ et W₆ , un astigmatisme orienté selon n'importe quel axe .

Pages spécialisées sur les polynômes de Zernike :