According to ref W1, a Dall-Kirkham telescope has a
diffraction limited flat-field nearly than can be approximated to the
one of a Newton having a F/D ratio equal to :
F/D Newton = 1.4 x m x F/D DK primary / sqrt (m2+1)
where :
F/D Newton = F/D ratio of the Newtionan telescope having the same diffraction limited flat-field
m = magnification factor of the DK secondary mirror
F/D DK primary= F/D ratio of the DK primary mirror
In the previous relation, the "m" secondary magnification factor have limited impact. The following figure is for m = 3:
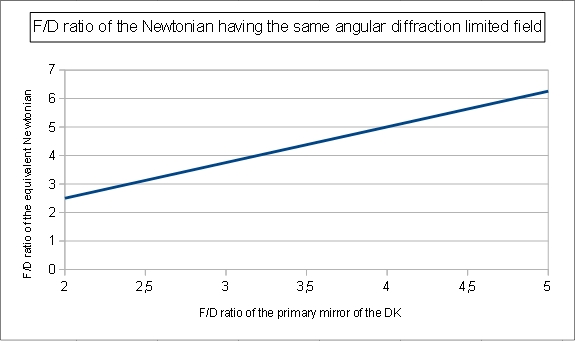
We will see in the following OLSO simulations that
the actual diffraction limited field departs a little bit from the
previous approximated value.
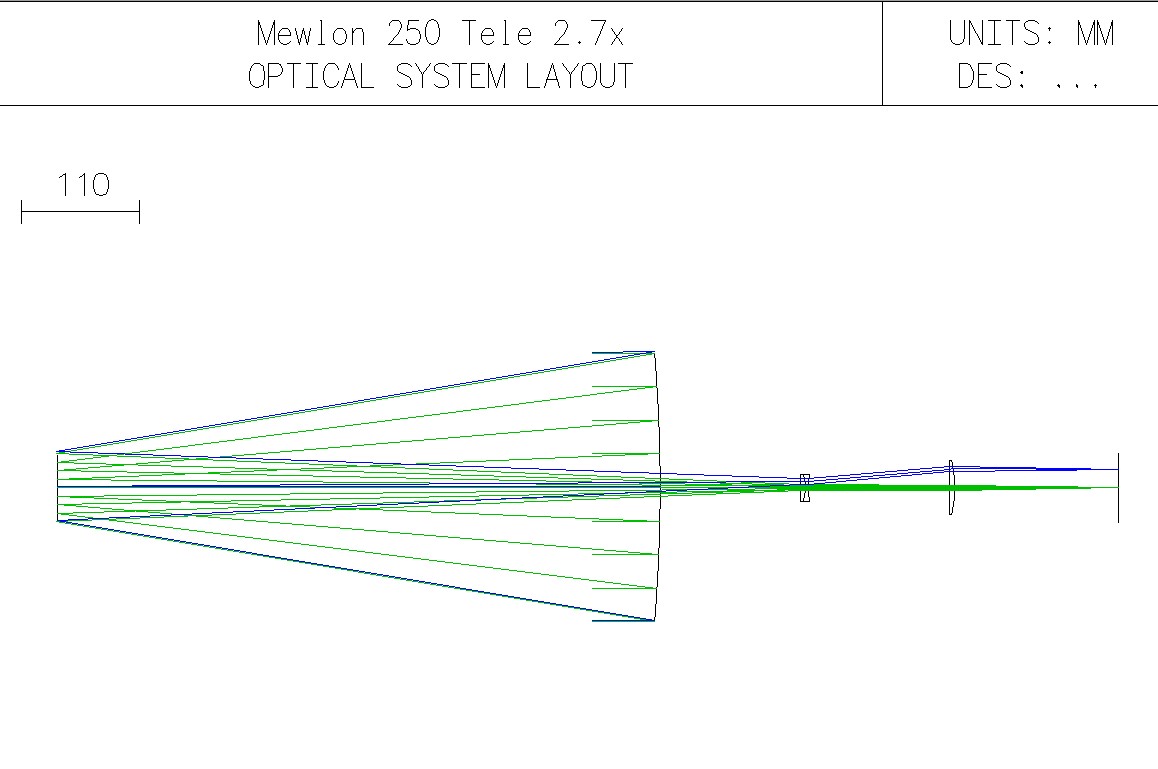
OSLO model :
From [1]
Radius of the diffraction limited flat field :
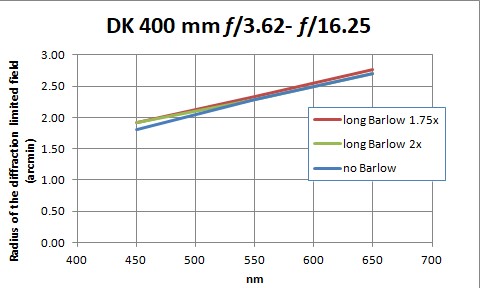
About 0.09° at 550 nm (from OSLO simulation). This is equivalent to a 200 mm F/5.4 Newtonian.
Radius of the diffraction limited flat field with the "2X long Barlow" :
Same as without Barlow lens from 400 to 700 nm (not simulated out of this range).
Field curvature :
- 413 mm (from calculation),
- higher magnification of secondary miroir increases field curvature,
- higher focal ratio on primary miroir decreases field curvature.
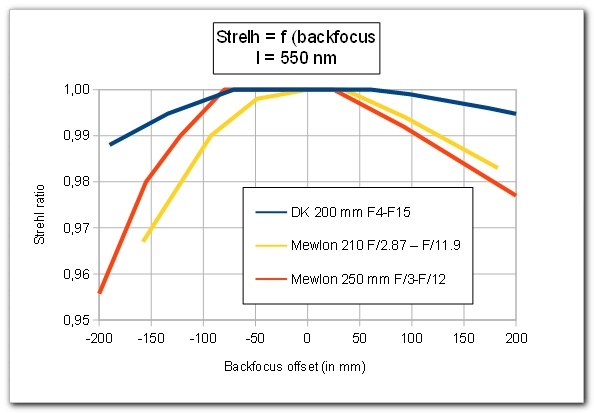
Sensitivity to backfocus (wavelength = 550 nm) :
This DK is pretty insentivive to reasonable
variations of backfocus ; the Strehl ratio keeps greater than 0.99 for
backfocus between -130 mm to + 170 mm from nominal back focus.
Sensitivity to radial off-centering of the secondary mirror :
An off-centering of the secondary miroir can be
pretty well corrected by adjusting the tilt of the secondary miroir as
shown in the three following figures :
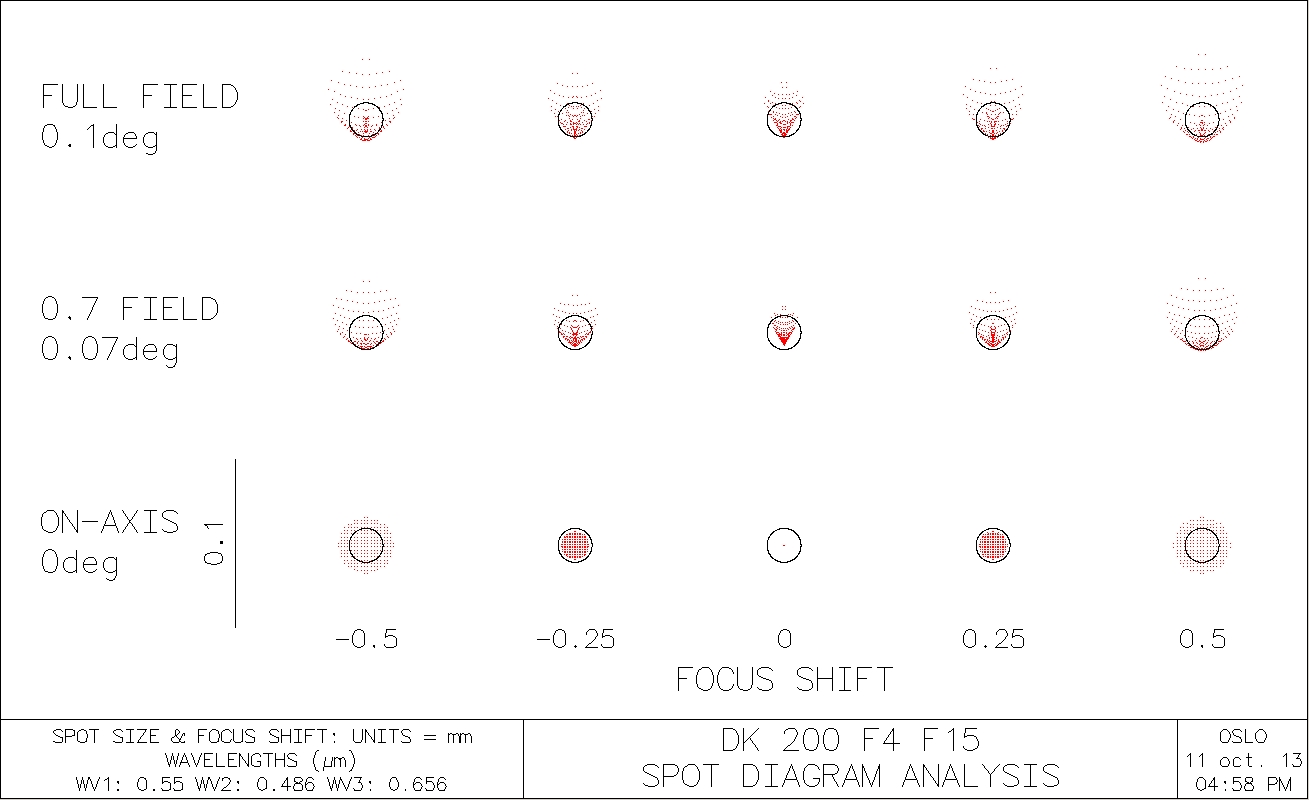
(a) Centered optics and nominal back-focus (550 nm) :
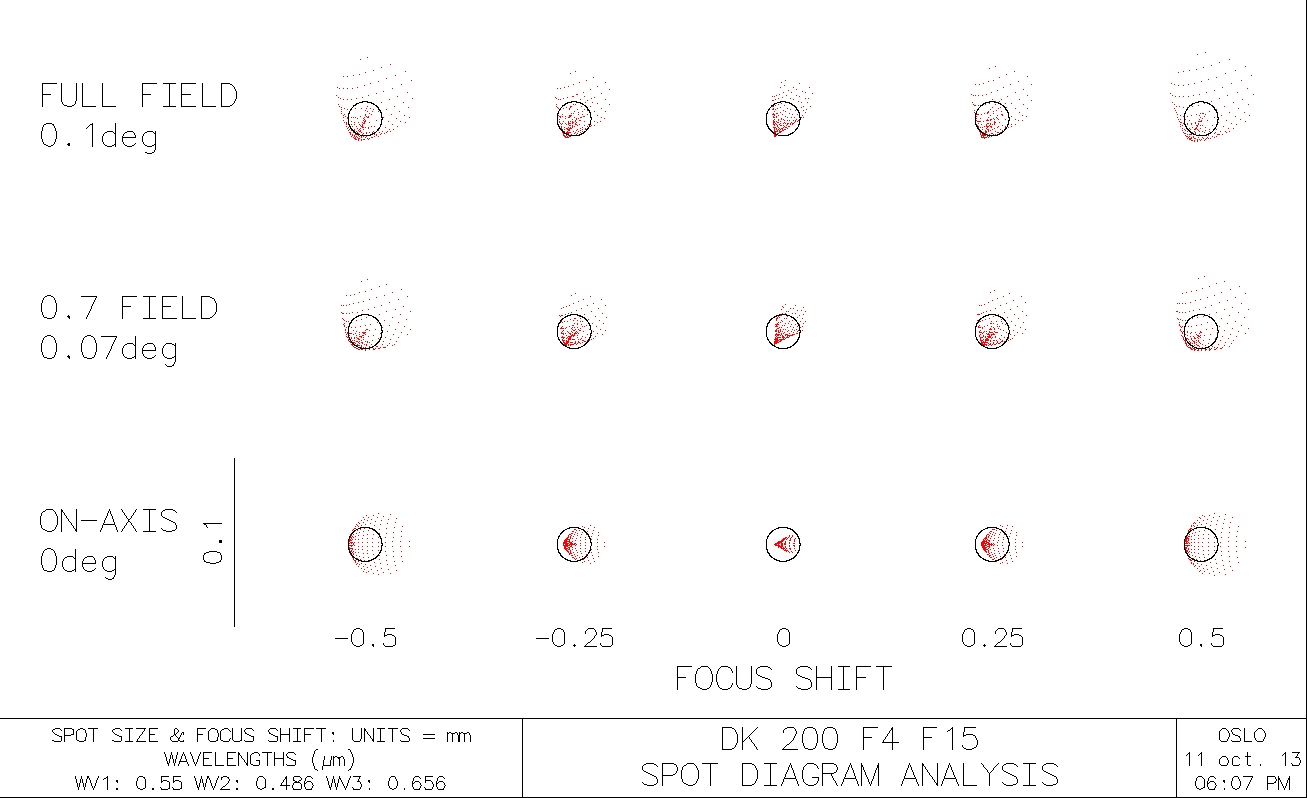
(b) With a 1 mm radial decentering of the secondary mirror (and refocussed on axis) :
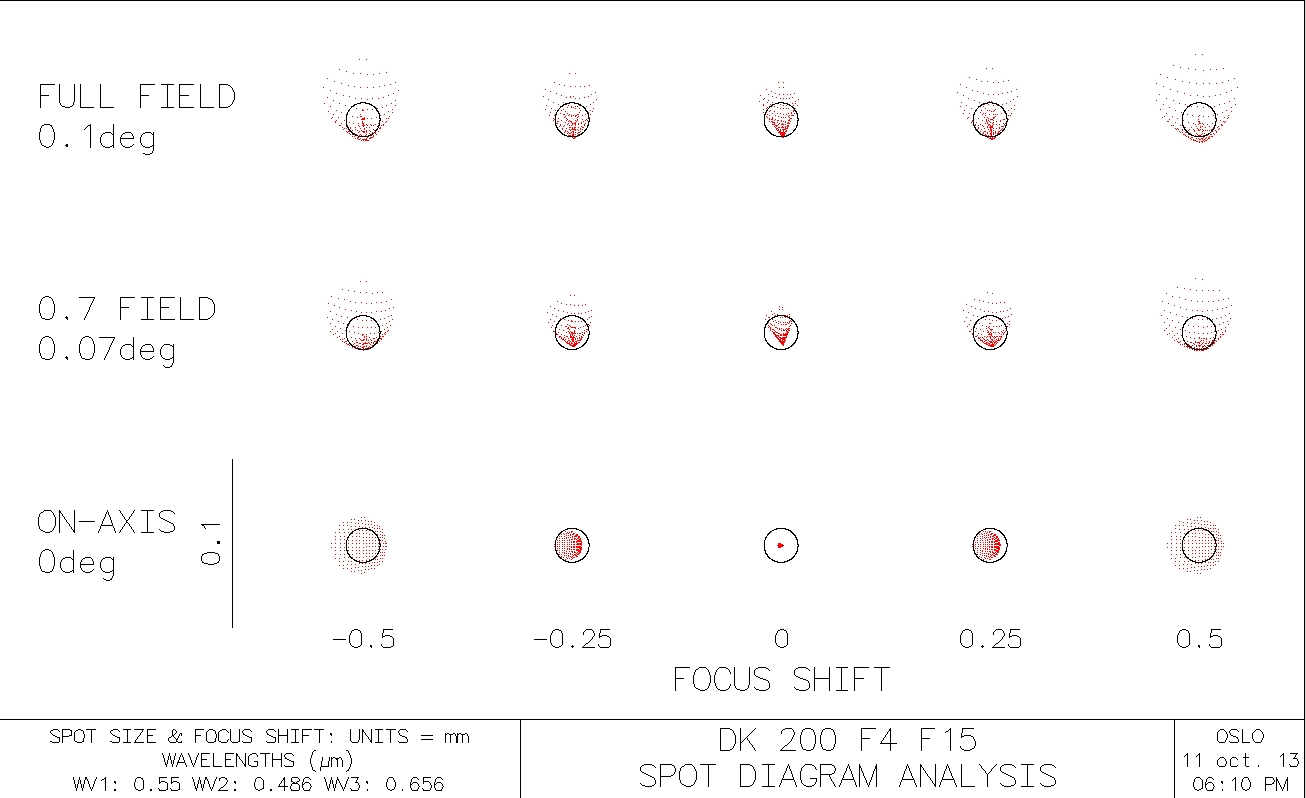
(c) With a 1 mm radial decentering of the
secondary mirror, and secondary mirror tilted by -0.13° to correct
on axis image (and refocussed on axis) :
The diffraction limited flat field in about 0.07° (in radius)
Takahashi Mewlon 210 mm f/2.9-f/11.9
OSLO model :
From Jocelyn Serrot and P. Cheyssac - Astrosurf Magazine n°48
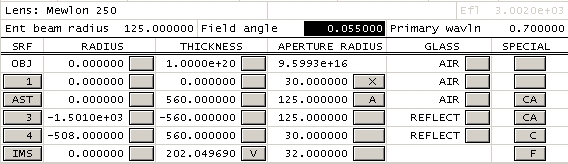
0.031° at 400 nm.
0.04° at 550 nm. This is equivalent to a 250 mm f/4.1 Newtonian.
0.037° at 400 nm.
0.049° at 550 nm.