Air-spaced Fabry-Perot etalon theoritical performances
3) Daystar filter modelling and additional results
4) Air-spaced F-P etalon theoritical performances and comparison with mica-spaced etalons
5) Analysis of the PST modification (air-spaced F-P etalon) and comparison between collimated and telecentric mounts
6) Contrast factor of the F-P etalon and blocking filter assembly
7) Contrast factor of the F-P etalon : test of various stacking schemes
8) Fabry-Perot math and bibliography
This part takes a look at the theoritical performances of air-spaced and composite solid air-space F-P etalon placed in front position (in front of the telescope aperture) and in a telecentric lens system.
The formulae of the F-P are from Fabry-Perot math and bibliography.
Information on solid air-spaced etalon are from US Patent 7142 573 B2 Nov 28, 2006.
Some comparisions are done with actual measurements made by Cyril Bazin and Serge Koutchmy of the Astrophysical Institute of Paris on Coronado F-P 40, 60and 90 mm (ref W11).
Coronado or Lunt Ha filters are air-spaced etalon. Noteworthy, a patent was passed by D. Lunt for a temperature compensated solid air-spaced etalon (US Patent 7142 573 B2 Nov, 2006). It is not clear whether Coronado actually implemented this solution in any of their products.
Composite solid air-spaced etalons present the double advantage of increased acceptance angle and thermal stability of the CWL. The idea is to partially fill the cavity with a solid parallel plate filler of refractive index n'. The filler is optically contacted to the one of the etalon mirrors. The refractive index of the resulting F-P etalon is the weighted average of the index of the air and solid plates.For teh record, some simulations are presented here, assuming a 1.4 refractive index for the composite solid air-spaced etalon.
The following parameters are taken from [W11] measurements :
- Air-spaced etalon
- Free Spectral Range = 9.57 A
- Finesse = 13.3 A
- FWHM= FSR / Finesse = 0.72 A
- Order of interference = 643
The modelling supposes that the CWL is equal to 6562.85 A at normal incidence, while measurement gave 6562.94 A.
The following figure compares the transmission curve of the modeled Coronado 0.7 A with the modeled 0.7 A mica-spaced F-P Daytar. The Daystar has a Free Spectral Range (= distance between peaks of tranmission) nearly twice as large as the Coronado:
FWHM and profile of the Coronado BF:
A blocking filter is used in order to select the peak of tranmission at 6563.85 A and cut the other transmision peaks.
1) The following measurement is courtesy from Peter Höbel (see additional measurements at http://www.sonnen-filter.de/), FWHM = 7.8 A.
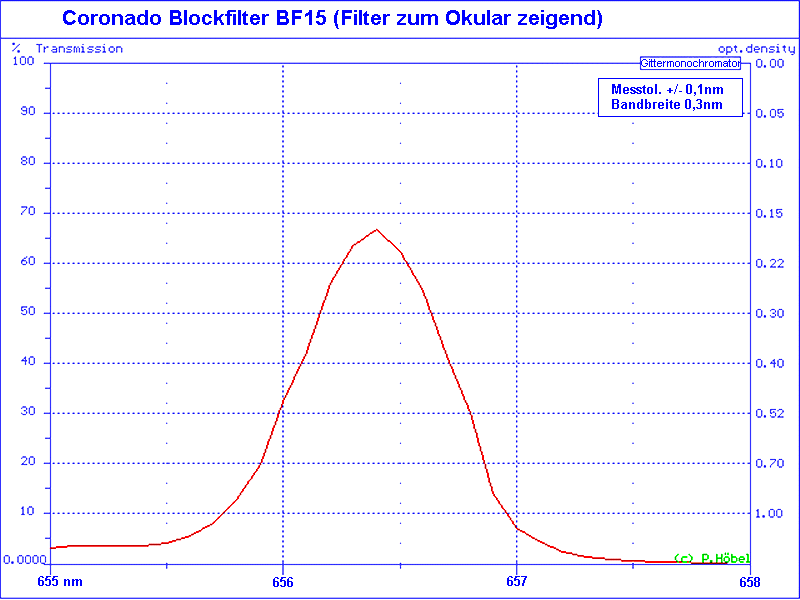
2) A measurement for the BF30 (Bazin and Koutchmy ref W11) gives FWHM = 7.5 A with a 30% peak transmission.
3) Another measurement by K.M. Harrison gives FWHM = 6.5 A.
4) I got the following results for the BF5 diagonal with Sol'Ex spectrometer: FWHM = 6.8 A (close to Ken result), CWL offset = +1.5A, 2-cavity filter.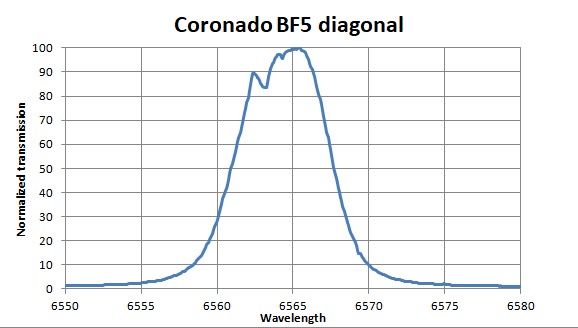
These values are significantly lower than for the FWHM of the blocking filters of mica-space etalon (DayStar or SolarSpectrum) because of the smaller FSR of air-spaced etalons.
The profile of the transmission curve of a one-cavity F-P is a Lorentz curve which means that the foot of this curve is rather large. In other terms the bandwidth measured at half maximum (FWHM) is only part of the story of the ability of the filter to select the chromosphere light (H alpha) and cut the photosphere light (every wavelenghts outside Ha). Obviously, the contrast between the chromosphere and the photosphere increases as the FWHM descreases, still ... there is a lot of "out band pass" light, ie. light from the photosphere that is transmitted by the F-P filter, because of this large foot (or "tail").
The profile is simular to a Daystar of 0.7 FWHM (not surprisingly ...)
The bandwidth at 10% transmission is three times wider than at 50% transmission. This is the classical value for one cavity F-P filter.
If we remember that the photophere is much brighter than the chromosphere, we can understand that the bandwidth at 10% (or even 5%) transmission will play an important role in the contrast of the Ha images.
One way to have a steeper profile is to double stack F-P filters. The FWHM of the double stacked Coronado is about 0.5 A, the transmission profile is steeper with a bandwidth at 10% equal to 2.3 FWHM (instead of 3 FWHM).
The following table gives the bandpass in function of the transmission level. These are the values for any perfect F-P etalon, air-spaced or not (Lorenztian transmission curve):
Transmission Bandpass
(simple stack F-P)
Bandpass
(double stack F-P of same FWHM)
E) CWL in function of the angle of incident light in a collimated beam :
From now on, it is necessary to make an assumption on the refractive index of the spacer. We will assume two values : n= 1 (for air-spaced F-P etalons) and 1.4 (for composite solid air-spaced F-P etalons).
If we assume Coronado filters are air-spaced, then a 1° tilt shifts the CWL by 1 A (versus 0.4 A for mica-spaced F-P etalon).
If we assume they are composite solid air-spaced, then a 1 ° tilt shifts the CWL by only 0.6 A.
F) Jacquinot spot and sweet spot (collimated beam with field angle) :
The Jacquinot spot is defined to be the region over which the change in wavelenght does not exceed sqrt (2) times the etalon bandpass. We can derive two expressions of Jacquinot spot :
with p = order of interference
F = finesse
q : in radians
For a 0.7 A Coronado 60 mm place in front prosition, and assuming an air-spaced F-P, we have p = 643 and F = 13.3, which gives an angle q = 1°, which is consistent (not surprisingly) with the transmission curves given above.
How this "Jacquinot spot" fits with the "sweet spot" of visual solar observers ? If we take a closer look at the transmission curves, we can see that the transmission at Ha for a 1° tilt is only 12%. Accordingly, the image will be dominated by the photosphere contribution.
If we want to keep the transmission in Ha greater than 60%, we have to limit the tilt of the air-spaced of the F-P etalon to 0.5°. This means that if the CWL is tunned on Ha on one limb of the sun, then the opposite limb will be blue shifted by 0.25 A, with a transmission of only 60% transmisison for Ha. If we have a composite solid-air space F-P etalon with a 1.4 equivalent refractive index, then the sweet spot increases to 0.7°.
G) Comparison with actual measurements (Coronado 60 mm placed in front position)
CWL shift = f (tilt)
The following measurements are courtesy from Cyril Bazin & Serge Koutchmy (see summary in W11). When the 4' light cone is considered in the calculation, the theory for an air-spaced F-P etalon comes in close agreement with the measurements.
The measurements for the Coronado 40 mm and 60 mm are essentially identical.
We can conclude that the Coronado 40, 60 and 90 mm are indeed air-spaced F-P.
Unfortunately, no PST has been yet measured.
H) Ai-spaced etalons: FWHM and CWL shift in function of f- ratio in a telecentric lens system
All the figures in this part are calculated by direct integration of the Lorentzian transmission of the Fabry-Perot etalon over the pupil of the telescope with a Julia program developped by the author. No approximation is made except the assumption that the etalon is assumed to be "perfect".
The assumed characteristics of mica-spaced etalons are FSR = 27 A and index n = 1.56, and for air-spaced etalon FSR = 9.3 A. These values are from measurements of actual mica-spaced and ai-spaced etalons with a spectrometer.Comparison of mica-spaced and air-spaced Fabry-Perot etalons :
The following figures compare the transmission profile of a 0.7 A air-spaced etalon (left) and a 0.7 A mica-spaced etalon (right) in telecentric systems of various f-ratio:
Air-spaced etalon Mica-spaced etalonBecause of the lower index (1 for air instead of 1.56 for mica), the air-spaced etalon requires a much higher f-ratio to perform properly. This is why professionals use very narrow air-spaced Fabry-Perot etalons in telecentric beams with f-ratio > 100
Air-spaced etalon Mica-spaced etalon
The following figures present the bandwith at 10% transmission, which is more relevant to the actual contrast provided by the filter:
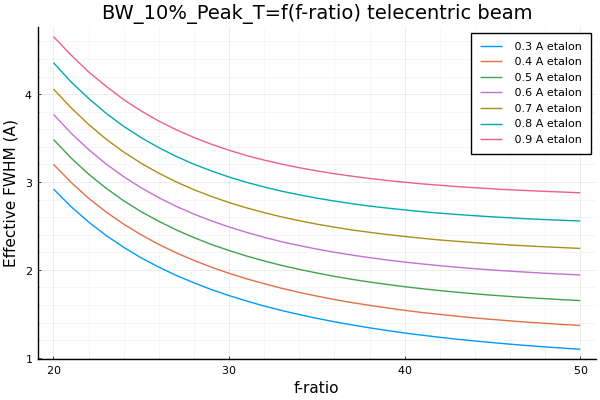
Air-spaced etalon Mica-spaced etalon
Finally, this figure presents the evolution of the CWL shift (to the blue) with f-ratio:
Link to the (FWHM, CWL, selectivity) = f (f-ratio) in text file
Conclusion on air-spaced F-P etalons :
a) Air-spaced F-P etalons work nicely when placed in front position (in front of the objective of a refractor). The sweet spot is large enough to cover the full disk of the sun with a limited CWL shift (< 0.25 A).
The only problem is the price of the etalon when its diameter increases ...
b) Placed in a telecentric beam at f/28, an air-spaced F-P etalon is a poor performer. It is better to use it at f/40 or higher.
c) Air-spaced F-P can also be used in collimated beam in internal position (see Lunt Ha refractors) or after the focal point. An example is the 200 mm Zeiss refractor of Rogerio Marcon with a Coronado 60 mm mounted in a collimated beam :
http://www.astroimagem.com/Mybestimages/Solaractivity.htm
An another example is the "PST modification" analysed here :