|
|
RGB VERSUS CMY
COLOR IMAGERY
The conventional method to restore the true colors of an astronomical object consists in combining three images carried out respectively through red (R), green (G) and blue (B) filters. These filters are known as additives, i.e. to obtain the trichromatic image it is necessary to add the intensity of the images corresponding to the spectral channel R, G and B.
There is another method to reconstitute the colors, well-known by photographers, who exploits a set of three filters known as subtractive: a cyan filter (C) which transmits the blue and the green, a magenta filter (M) which transmits the blue and the red, a yellow filter (Y) which transmits the green and the red. The method to restore the true colors image is more complex than in the case of traditional imagery RGB. It is necessary to calculate differences in intensities to obtain the components R, G and B, essential for a display true colors on the computer screen (this is the reason of the subtractive name for CMY combination).
The set of equations to be applied to each pixels allowing to constitute triplet RGB starting from an observation carried out through filters CMY is:
R = Y + M - C
G = Y + C - M (1)
B = C + M - Y
Figure 1 shows the transmission characteristic of a set of RGB filters and a set of CMY filters. They are interferential filters from EDMUND SCIENTIFIC (www.edmundoptics.com). The reference of the RGB set filters in diameter of 50 mm is K52-547 (price: $68.70) and the reference of the CMY set filters, always in diameter of 50 mm, is K52-550 (price: $68.70). It will be noted that the transmission of these filters is excellent and that the quality to price ratio is very nice.
|
|
Figure 1. On left, an additive set filters. On right-hand side, a subtractive set filters (documentation Edmund Scientific).
The imaging through CMY filters is particularly popular in the United States. Many amateurs on the other side of the Atlantic swear only by this technique. Which is the advantage of CMY filters compared to RGB filters?
The interest which jumps immediately to the eyes is that for a same exposure time, CMY filters make it possible to record approximately twice more signal in each RGB channel. For example, the blue part of the spectrum is observed at the same time when the filters cyan and magnenta are used, whereas it is only one time with a traditional RGB set filters (when the filter B is used). The conclusion of some US colleagues is that it is possible to expose twice less with filters CMY compared to filters RGB for an identical result. We will see further if we can confirm this result...
Another drawbacks of RGB filters is that cut-off zone does not allow the detection of certain spectral lines like for nebulae imaging which present emission lines (planetary nebulae, diffuse nebulae). This problem disappears with CMY filters. For this reason, the example of RGB filters of figure 1 is rather characteristic since the filter B and the filter G overlap just at the wavelenth of the significant line [OIII] at 500.7 nm. On the other hand, the cyan filter of CMY combination lets pass this spectral line without disturbance. Therefore favours with filters CMY... but not so simple!!! The examination of figure 1 shows that with RGB combination the line [OIII] is observed at the same time with the B filter and the G filter, so the signal of the line in these two bands is thus added at the time of the constitution of the true colors image. The transmission for these two bands on the level of oxygen line is about 60%. At the same time, the noises of these two images are added quadratically and it is shown that, in the particular case, the equivalent transmission of the R and G band at the oxygen wavelength is equal to SQR(2) x 60% = 1,414 x 60 % = 85% (SQR = square root). The merge of the bands is particularly favorable for [OIII] observation with Edmund RGB filters. The transmission of the cyan filter towards 500 nm is 87%. Lessons learned: the signal to noise ratio of an image of nebula observed in the line [OIII] is thus almost identical that one uses a good combination RGB or combination CMY!
When using RGB filters or CMY filters, attention should be paid to restore the chromatic balance of the observed object. Simplest is to observe star of a Solar type through filters RGB and CMY, and to determine a set of coefficients to apply to the pixels of components RGB channel in such a way that the standard star is restored to white on the screen. Table 1 hereafter gives a star list of the spectral type near to that of the Sun (G2V) and especially to which index color is very close to our star. These stars are often used to calibrate the photometric observations of solar system objets (comets, asteroids, planets). It is pointed out that for the Sun we have: B-V=0.674 and V-R=0.505.
Table 1. Stars similar to the Sun (see for example
http://www.lowell.edu/users/jch/workshop/sa.html & Hardorp J. 1978,A&A, 63, 383)
HD |
RA |
DEC |
Sp |
V |
B-V |
V-R |
1835 |
00 22.9 |
-12 13 |
G2V |
6.402 |
0.660 |
0.537 |
4915 |
00 51.2 |
-05 02 |
G0V |
6.982 |
0.666 |
0.543 |
8262 |
01 22.3 |
+18 41 |
G3V |
6.973 |
0.630 |
0.513 |
10307 |
01 41.8 |
+42 37 |
G1.5V |
4.965 |
0.623 |
0.499 |
|
20630 |
03 19.3 |
+03 22 |
G5V |
4.83 |
0.68 |
|
|
28099 |
04 26.7 |
+16 45 |
G2V |
8.09 |
0.657 |
|
34411 |
05 19.1 |
+40 06 |
G2V |
4.705 |
0.622 |
0.499 |
|
44594 |
06 20.1 |
-48 44 |
G3V |
6.61 |
0.66 |
|
|
76151 |
08 54.3 |
-05 26 |
G2V |
6.01 |
0.68 |
|
|
78418 |
09 08.8 |
+26 38 |
G5IV |
5.98 |
0.65 |
|
|
86728 |
10 01.0 |
+31 55 |
G3V |
5.40 |
0.65 |
|
89010 |
10 16.5 |
+23 30 |
G1.5V |
5.968 |
0.668 |
0.529 |
95128 |
10 59.5 |
+40 26 |
G0V |
5.037 |
0.622 |
0.505 |
126053 |
14 23.3 |
+01 14 |
G1V |
6.266 |
0.644 |
0.527 |
133002 |
14 50.3 |
+82 31 |
F9V |
5.643 |
0.682 |
0.555 |
141004 |
15 46.4 |
+07 21 |
G0V |
4.419 |
0.611 |
0.494 |
|
144585 |
16 07.1 |
-14 04 |
G5V |
6.32 |
0.66 |
|
146233 |
16 15.6 |
-08 22 |
G2V |
5.499 |
0.650 |
0.524 |
159222 |
17 32.0 |
+34 16 |
G5V |
6.537 |
0.646 |
0.510 |
177082 |
19 02.6 |
+14 34 |
G2V |
6.895 |
0.641 |
0.518 |
|
181655 |
19 19.6 |
+37 20 |
G8V |
6.31 |
0.68 |
|
186408 |
19 41.8 |
+50 32 |
G1.5V |
5.986 |
0.659 |
0.521 |
186427 |
19 41.9 |
+50 31 |
G2.5V |
6.244 |
0.671 |
0.531 |
187237 |
19 48.0 |
+27 52 |
GIII |
6.896 |
0.654 |
0.512 |
|
191854 |
20 10.2 |
+43 56 |
G5V |
7.45 |
0.56 |
|
193664 |
20 17.5 |
+66 51 |
G3V |
5.932 |
0.601 |
0.497 |
197076 |
20 40.8 |
+19 56 |
G5V |
6.444 |
0.628 |
0.505 |
217014 |
22 57.5 |
+20 46 |
G2.IV |
5.459 |
0.676 |
0.517 |
222143 |
23 38.0 |
+46 12 |
G5 |
6.591 |
0.652 |
0.522 |
I have observed star HD159222 with Takahashi refractor FSQ-106 (4-inch diameter, F/D=5) through filters sets RGB and CMY from Edmund Scientific. The camera is an Audine equipped with a KAF-1602E CCD. A KG3 IR-rejection filter was systematically added to secure inopportune increase of the interferometric filter transmission in the infrared part of the spectra. To carry out a good photometry it is necessary to use a relatively long exposure time in order to integrate the fluctuations signal caused by atmospheric scintillation. The exposure time selected is 20 seconds and it is common to all the filters. Taking into account the brightness of HD159222 it was necessary to defocus star image to avoid detector saturation (see figure 2).

Figure 2. Defocused image of star HD159222. Photometric
measurements were carried out with the technique of aperture photometry (PHOT command of the Iris software).
Table 2 gives in unit of count (ADU - Analog Digital Unit) the value of the signal integrated in 20 seconds through RGB filters, as well the normalization coefficient (or weight) to be applied to the pixels of RGB images to correct the chromatic balance for a solar type star. For example for the image R we have 363628/576369=0.631 (here the arbitrary reference image is the blue image).
Table 2. Result of the observation of star HD159222
with RGB filters.
Filter |
ADU |
Coefficient |
R |
576369 |
0.631 |
G |
380824 |
0.955 |
B |
363628 |
1.000 |
Table 3 gives the value of the signal found through CMY filters.
Table 3. Result of the observation of star HD159222
with CMY filters.
Filter |
ADU |
C |
828661 |
M |
824928 |
Y |
1171421 |
From the elements of table 3 we calculate the signal in RGB channels starting from the set of equation (1) and also the corresponding normalization coefficients to correct color of a Solar-analog star (see table 4).
Table 4. Signal in RGB bands calculated starting
from observations CMY (see equations (1)).
Band |
ADU |
Coefficient |
Coefficient relative to RGB set filters |
R |
1167688 |
0.413 |
0.311 |
G |
1175154 |
0.410 |
0.309 |
B |
482168 |
1.000 |
0.754 |
Note that the signal measured by using only KG3 filter is of 1605842 ADU.
The coefficient otbained by this method are now going to be used for chromatic balance of all images, for example on M51 as described below.
Figure 3 shows M51 images through RGB filters and the corresponding trichromatic image by using FSQ-106 refractor and by combining for each filter 4 images of 180 seconds integration times (and the TRICHRO command of Iris). The coefficients of table 2 were applied (i.e. all the pixels of the R image resulting from the addition of 4 x 180 seconds exposure time elementary images were multiplied by the weight 0.631 and that all the pixels of the image V were multiplied by 0.955 ; we use for this the command MULT). For an optimum processing it should be taken care that the reference solar-type star is taken with the same zenith height as the object studied in order to not introduce effect of differential chromatic absorption of the atmosphere. This condition was observed with a sufficient approximation here. After multiplied the channels with the adequate normalization coefficients it is necessary to harmonize the sky background while adding or by subtracting a constant with all the pixels from each channels in order to avoid giving dominant color on the sky level (see commands OFFSET or NOFFSET for example). It still should be noted that the images were obtained in an urban environment (magnitude of the sky of 17 by square arcsecond in the V band).
Figure 4 shows the same result (calculated
RGB channels) for identical protocol carried but through CMY filters. The CMY
images are converted to RGB images by the command CMY2RGB.
The calibration coefficients of table 4 were applied.
|
|
|
|
Figure 3. Of left on the right: image R, image G, image B, tricolor image (synthesized with command TRICHRO).
|
|
|
|
Figure 4. Of left on the right the tapes R, G and B calculated starting from images CMY (command CMY2RGB), and corresponding tricolor image.
No dominant abnormal color affect the tricolor images of figures 3 and 4. Moreover, the balance of the colors of these two images is extremely similar what is the sign that the calibration procedure starting from a Solar-analog star is working properly. The trichromatic image resulting from data CMY appears slightly denser, but the choice of the thresholds of visualization plays a role here. For better apprehending the difference between these images it is a good idea to try an analysis of the signal to noise ratio in the two situations.
We will simplify by considering that the noise is primarily dominated by the signal itself, i.e. that the reading noise of the CCD is negligible. That does not changes basically the results and in any case, it is this photon noise regime which dominates in the analyzed images which were obtained in suburban environment ( the sky background having a level very high).
First of all, let's analyze the case of a tricolor image resulting from RGB filters. For a given pixel one can consider that the signal S is the sum of the 3 tricolor components:
S = R + G + B
In photon noise dominant situation, the noise N is:
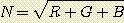
The signal to noise ratio is thus equal to:
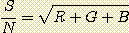
Let us see now the case of a trichromatic image synthesized starting from CMY filters. Is R', G' and B' the RGB channels calculated starting from the images taken through CMY filters (CMY2RGB command). According to the equations set (1) we have:
R' = Y + M - C
G' = Y + C - M
B' = C + M - Y
and:
S = R' + G' + B' = Y + M - C + Y + C - M + C + M - Y = C + M + Y
The noise associated with calculation of each channels R', G' and B' is equal to the quadratic sum of the noises of the images C, M and Y (the evaluation of the signal for a channel utilizing two additions and one subtraction and note that the signal is uncorrelated for the different images). This noise is identical for the three channels and is equal to:
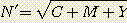
The production of the tricolor image requires the three channels R', G' and B', so the final noise is then:
N = SQR(3) . N' = SQR(3 . (C + M + Y))
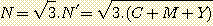
The signal to noise ratio is thus equal to:
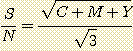
By noting that in theory one must have:
C = G + B
M = R + B
Y = R + G
the preceding equation becomes:
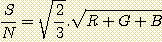
The coefficient 2 which appears in this equation traduct the fact announced to the beginning of this paper that imagery CMY makes it possible to acquire twice more signal in spectral bands RGB than can provide directly a filter set RGB.
While comparing with the value of the signal to noise ratio in the case of the use of filters CMY it appears that subtractive technique RGB brings a profit of:
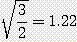
In other words, for identical exposure time, use of RGB filters increases signal to noise ratio of 22% compared to use of CMY filters. One supposes here that these two sets of filters produce equivalent losses by absorptions and reflexions and that R=G=B and C=M=Y at the output of the CCD camera. This simplified analysis shows that the use of CMY filters does not authorize to decrease the exposure times by a factor two compared to traditional filters RGB and there is no gain to use CMY filters in this situation!
We now will take into account in the readout noise of the CCD (and eventually the noise generated during the processing). This noise is s. We will also consider the transmission of the various filters and CCD responsivity (for a star G2V) in the form of the coefficients necessary to obtain the chromatic balance of thetri-color image. These coefficients are Kr, kg and Kb, calculated in tables 2 and 4. After application of these coefficients we have R=G=B. We define the parameter Q:
Q = R = G = B
The signal to noise derived from the use of filters RGB is now:
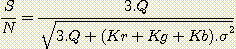
The signal to noise derived from the use of filters CMY is:
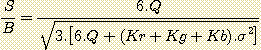
Let us consider the following application: after the application of the coefficients of normalisation Kr, Kg and Kb we have Q=1000 electrons. The noise of the camera is estimated at 20 electrons. Let us make the numerical application in the case of the use of filters RGB. We have (see table 2):
Kr = 0.631
Kg = 0.955
Kb = 1.000
and:
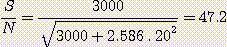
With filters CMY we have:
Kr = 0.311
Kg = 0.309
Kb = 0.754
(it is necessary to use the coefficients which produces a final image of identical intensity in the two configurations in order to be able to compare the performances)
and:
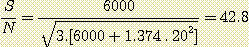
The RGB configuration continues here to give a signal to noise higher than CMY configuration (47.2/42.8=1.10, so a gain of 10% approximately).
If calculation is remakes for a signal of Q=R=G=B=100 electrons only (very very dark background) the situation reverses:
For filters RGB one finds S/B=8.2
For filters CMY one finds S/B=10.2
So the winner is CMY set filter (gain of 24% because the transparency of my CMY filters seem better then RGB)
But on average there is very little difference between the two set of filters and the advantage of CMY technique is never decisive.
One will note to finish that the weight coefficients in the case of CMY imaging technics are definitively not similar from each to other than those corresponding to RGB imaging (see table 2 and 4). It is necessary in particular to apply a weight raised to the channel B compared to the channels R and G with the subtractive filters. The resulting effect is an apparent increase in the noise in the image B calculated with CMY component compared to the B channel obtained directly starting from a B filter. It is particularly obvious while comparing on figures 3 and 4. This addition of noise in the B band is quite perceptible specially if one seeks to visualize the weak details of the image (see figure 5).
|
|
Figure 5. Visualization with high contrast of the tricolor images, on the left, additive imagery RGB, on the right, subtractive imagery CMY. Note that the noise of the channel B is more visible in this last image. But note also that the global S/N ratio is very similar between these images (better for low light in the case of CMY, better for moderate intensity pixels for RGB).
Figure 6 is the sum of tricolor images RGB and CMY applied to the area of M51, and shows the field of galaxy around this famous object.

Figure 6. Part of the color image carried out with
FSQ-106 refractor and the Audine camera equipped with a KAF-1602E. The dynamic
range of the image was modified by using DDP command of Iris (click on the image
to display the original format).
It should be still underlined that filters CMY can be at the origin of a loss of resolution because of the presence of the atmospheric phenomenon of refraction (it is easier to correct the effect with RGB images obtained directly). Also, obtain images correctly calibrated for a scientific application (calculation of the color equations) is very problematic from CMY images.
In conclusion, the use of CMY subtractive filter in the place of RGB filter is a valid option to carry out realistic color images of astronomical objects. It is noted that the first configuration allows a benefit in signal to noise ratio only for very faint objets and in my peculiar case of transmission filter (these is dispersion in the transmission curve of different sets filters). However this gain is not high in this peculiar situation. The reason comes from the contribution of noise because of the arithmetic operations between images to extract RGB components starting from the observations carried out through CMY filters. In the example shown here it appears that the chromatic balance is more homogeneous with filters RGB than with CMY filters (that indicates that it would be necessary to integrate signal longer through filters cyan and yellow compared to the magenta filter). The problem involved in the recovery of the spectral lines in the case of RGB imagery is not necessary real. Lastly, whatever the technique is used, it is very simple to calculate the calibration coefficients to be applied to the images starting from a star similar to the Sun to obtain images having a pleasant visual aspect having a colors balance close to the visual apparence that a human eye would perceived it (but remember reserve for scientific use of the CMY data...).
For discussions about other techniques concerning
color images click here (LRGB).