CWL and FWHM in non telecentric systems
1) Center Wave Length (CWL)
and bandpass (FWHM) as a function of f-ratio of the telescope and
tilt of the F-P filter (in collimated beam, telecentric beam or
non-optimized telecentric system)
2) CWL shift and FWHM broadening in non telecentric systems (refractors and Cassegrain telescopes) and useful formulae
3) Daystar filter modelling and additional results
4) Air-spaced F-P etalon theoritical performances and comparison with mica-spaced etalons
5) Analysis of the PST modification (air-spaced F-P etalon) and comparison between collimated and telecentric mounts
6) Contrast factor of the F-P etalon and blocking filter assembly
7) Contrast factor of the F-P etalon : test of various stacking schemes
8) Fabry-Perot math and bibliography
Refractors with Barlow lens
This section compares different non telecentric lens systems having the same F/30 resulting ratio :
- a 150 mm f/30 refractor,
- a 150 mm f/7.5 refractor with a "long" 4× Barlow lens of -127
mm focal length (equivalent to the focal lenght of the old
2× Astrophysics Barlow lens),
- a 150 mm F/7.5 refractor with a "short" 4× Barlow lens of - 55 mm focal length (equivalent to Baader FFC).
Optical configuration
The introduction of a Barlow lens in the optical path results in an increase of the field angle (theta 2):
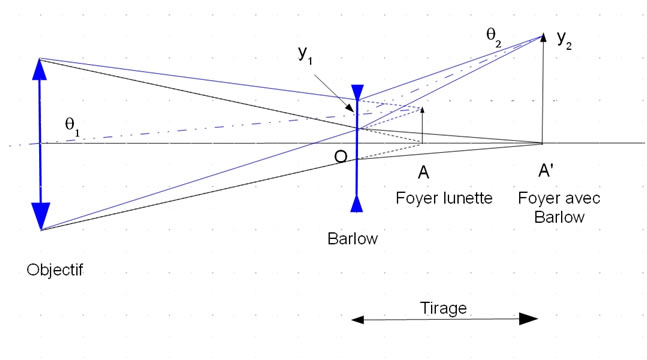

The magnification factor of the field angle converges to F/f when the magnification factor of the Barlow M increases (i.e. collimated beam such as in the PST modification).
CWL shift and FWHM broadening:
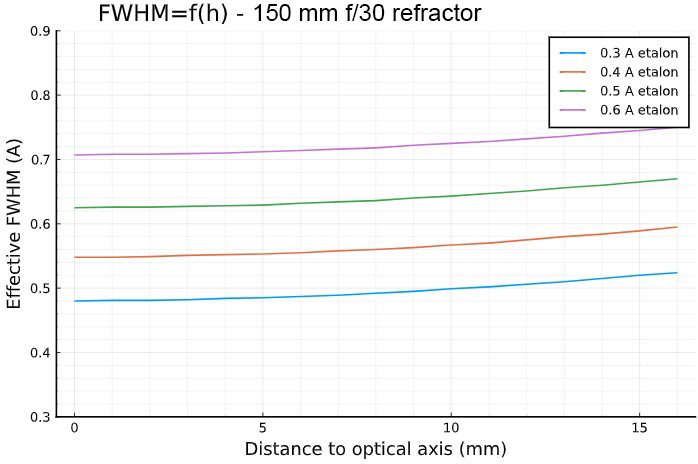
- left column: effective FWHM and CWL shift, in function of the distance from the optical axis, for a 150 mm f/30 refractor,
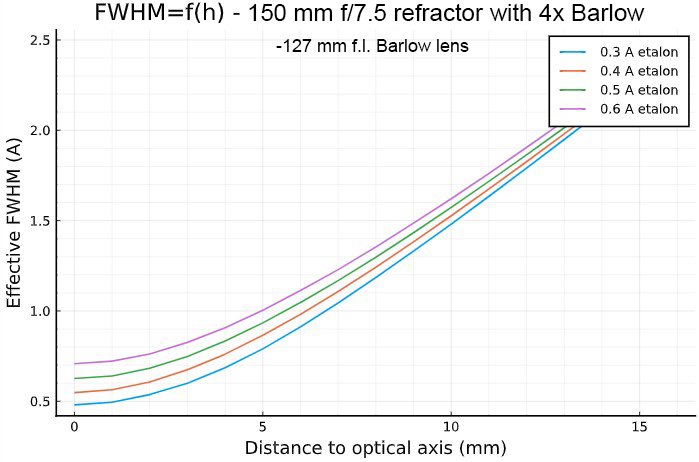
- center column: effective FWHM and CWL shift, in function of the
distance from the optical axis, for a 150 mm f/7.5 refractor equiped
with a "long" 4× Barlow lens (f.l.= -127 mm),
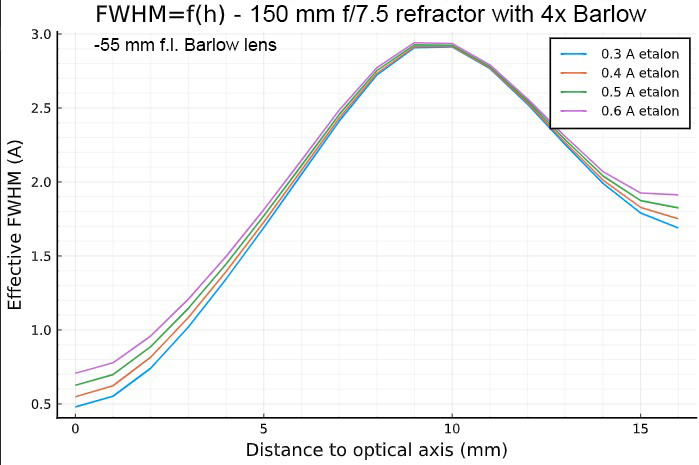
- left column: effective FWHM and CWL shift, in function of the
distance from the optical axis, for a 150 mm f/7.5 refractor equiped
with a "short" 4× Barlow lens (f.l.= -55 mm).
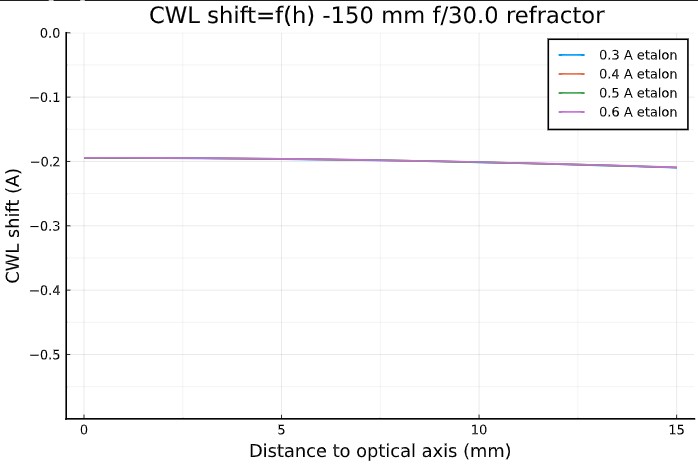
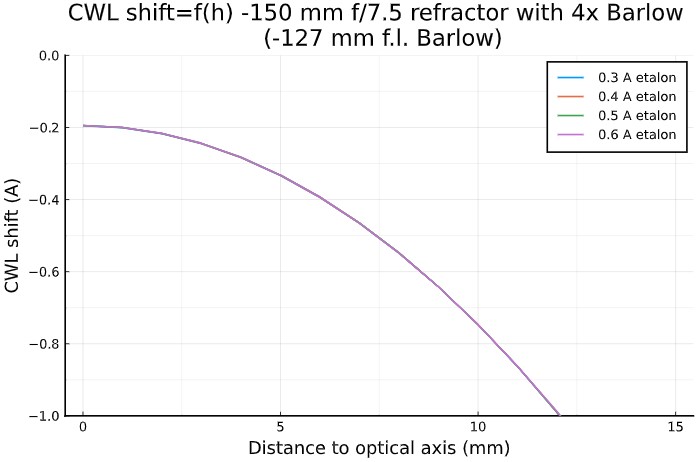
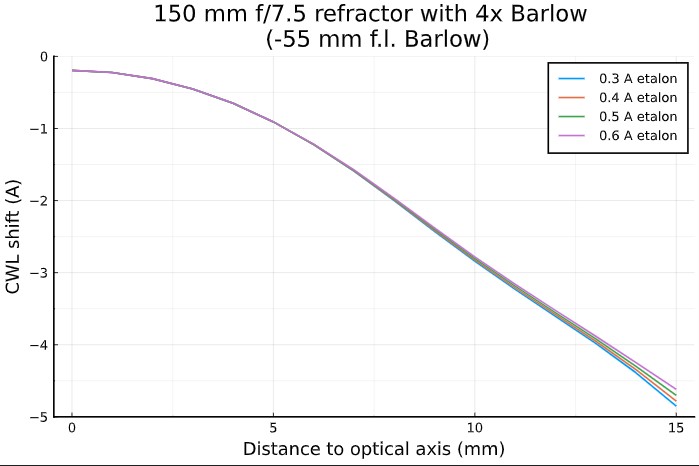
We can see that :
- A 150 mm f/30 refractor performs quite well for Ha
observations with a mica-spaced F-P etalon.
- However, a 150 mm f/7.5 refractor
using a 4× Barlow would have a very small sweet spot.
Most of the field of view would be away from Ha and would suffer a
very large FWHM. The situation is even worse with short focal length Barlow lenses because of the increased field angle.
Sensitivity of CWL shift and FWHM broadening with filter tilt
Simulation for a 150 mm f/30 refractor and a 0.25° filter tilt:
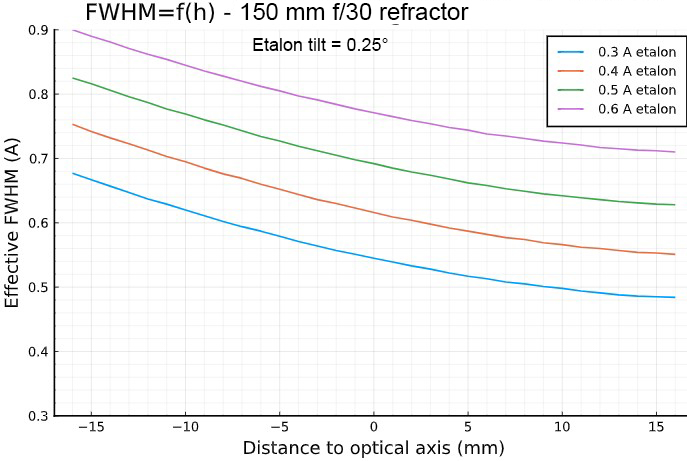
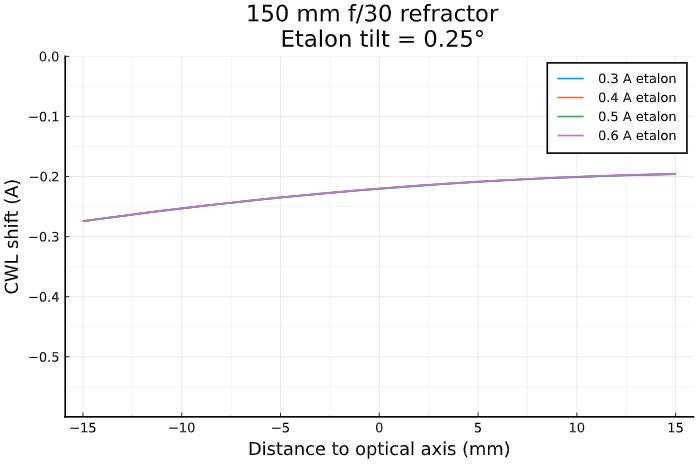
Simulation for a 150 mm f/7.5 refractor equiped
with a "long" 4× Barlow lens (f.l.= -127 mm), and with a 0.25° filter tilt:
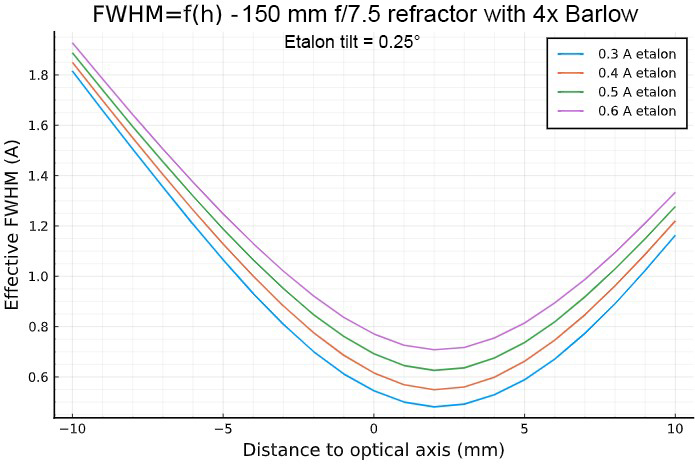
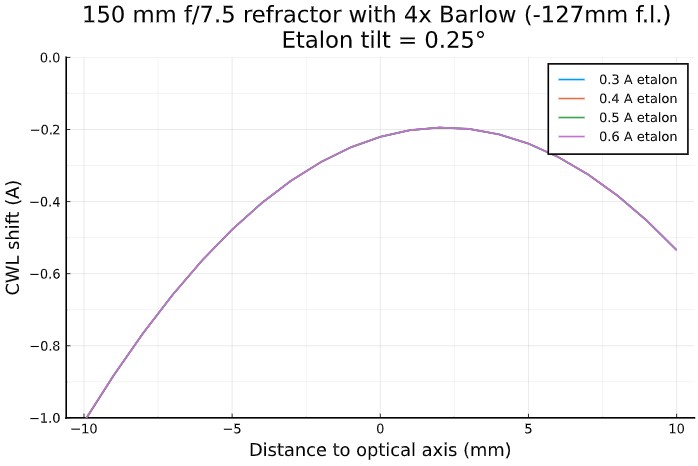
The situation is much worse if a Barlow lens is need to reach the f/30 ratio.
By comparison the FWHM in a f/30 telecentric beam and 0.25° etalon tilt
would be uniform accross the field of view and equal to :
- 0.55 A for a 0.3 A mica-spaced etalon,
- 0.61 A for a 0.4 A mica-spaced etalon,
- 0.68 A for a 0.5 A mica-spaced etalon,
- 0.77 A for a 0.6 A mica-spaced etalon.
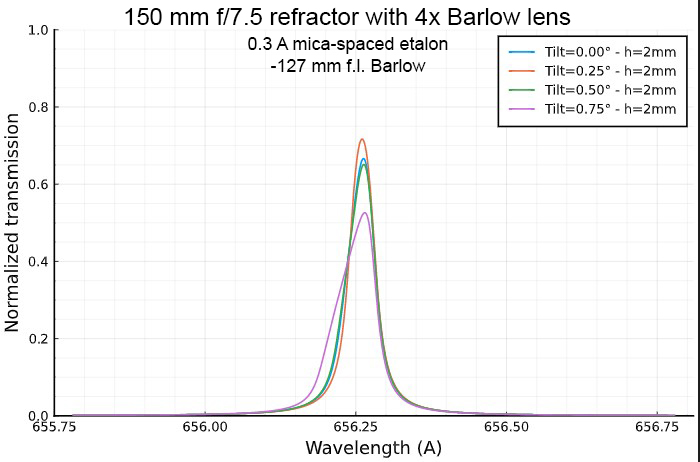
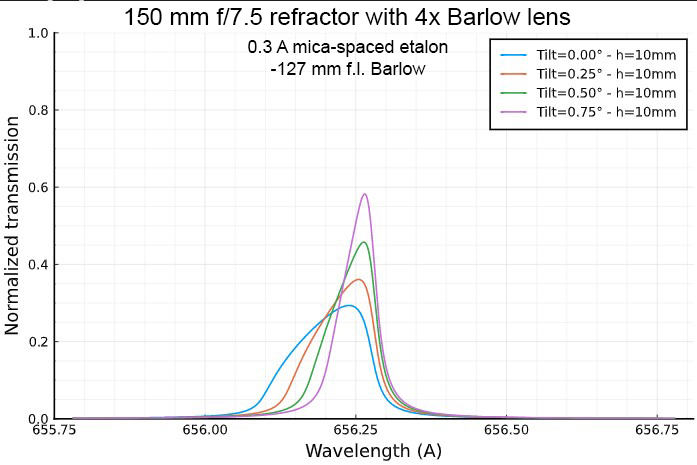
Transmission profile of a 0.3 A mica-spaced etalon at the focus of 150
mm f/7.5 refractor equiped
with a "long" 4× Barlow lens (f.l.= -127 mm), for three
different distances for the optical axis, and for four tilt angles:
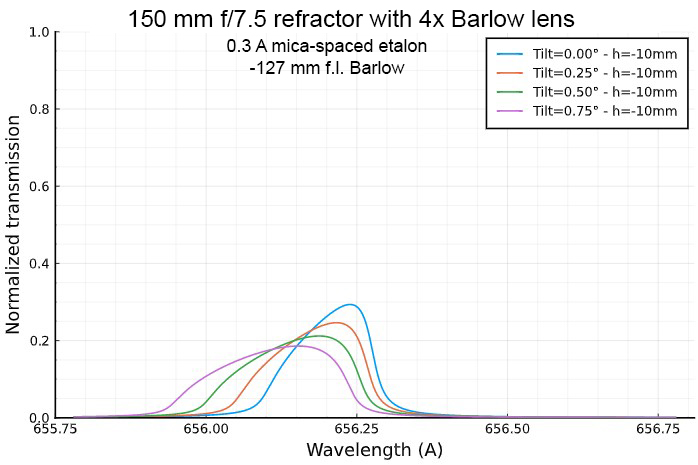
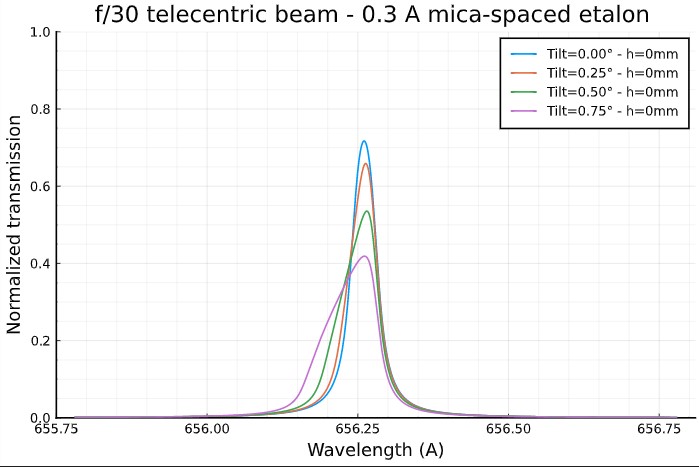
For comparison, tranmission profile of a 0.3 A mica-spaced etalon in a f/30 telecentric beam:
3) Conclusion:
In any case, the use of a telecentric mount to reach f:/30 is far more preferable than the use of a Barlow lens.
Cassegrain telescopes
Thie secondary mirror plays the same role as the Barlow
lens. The previous formula given the magnification factor of the field
angle still holds (f beeing the absolute value of the secondary mirror focal length).
Let's take the example of an hypothetical Dall-Kirkhan 250 mm f/3-f/27 telescope having the following characteritics :
D = 250 mm
F = 750 mm (ie. f/3 ratio for the primary mirror)
f = 243 mm
M = 9 (ie.resulting focal ratio = 9 × 3 = 27)
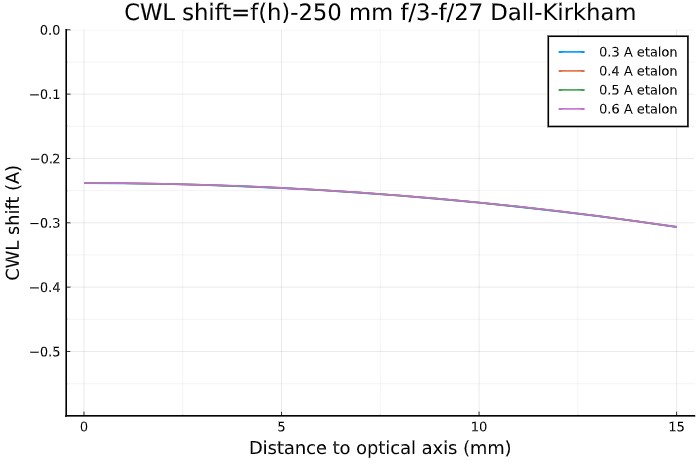
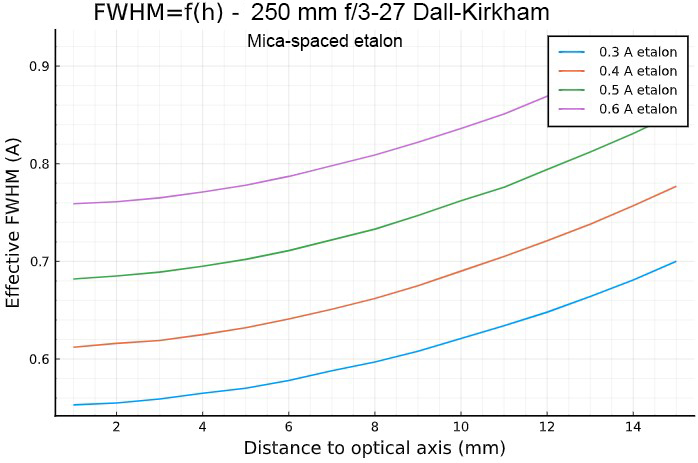
The FWHM broadening away the optical axis is due to the
field angle and to the field angle magnification factor. It is larger
than the FWHM of the 150 mm f/30 refractor, but smaller than the 150
f/7.5 refractor equiped with a 4× Barlow lens, because of the
longer focal length of the secondary mirror (-243 mm) compared
the 4× Barlow lens (-127 mm).
NB : the FWHM on the optical axis is set by the f/27
ratio. It is identical to the one resulting from a
f/27 telecentric system.
Performance of an etalon in a convergent beam : some useful formulae (telecentric/non telecentric beam, tilted/non tilted filter)
CWL shift and FWHM broadening in a convergent beam and with a field angle
Most of the simulations presented in these web pages are calculated by direct integration of the
Lorentzian transmission curve over the pupil of the telescope using a
Julia program developped by the author. No approximation are made in
these simulations except the assumption that the etalon was "perfect".
However, in this section, we provide usefull simplified (though very
accurate) formulae to calculate the CWL shift (to
the blue) and a FWHM broadening in a convergent light beam (telecentric or not, filter tilted or not). They
are taken from chapter 7 of "Thin Film, optical filters, H Angus MacLeod, IoP, Third Edition, 2001, page 288- 291".
Three cases are defined depending on the geometry of the light beam falling on the filter surface:
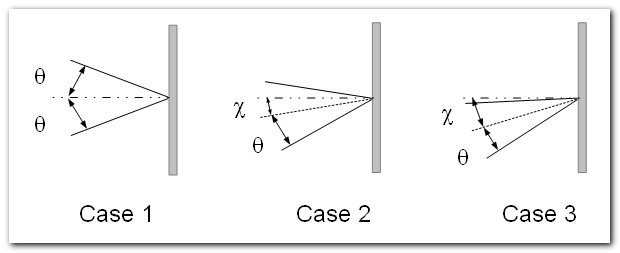
The associated formulae for the CWL shift and FWHM broadening (3) are:

Let's try to decipher these three cases and associated formulae. First, the notations :
- the incident beam of light is a converging cone of light whose half angle is set by the f-ratio ratio : q = D / 2F.
- the axis of the cone of light strikes the F-P at an angle c from normal incidence. This angle is called the "field angle".
Now, let's have a closer look at the three cases :
- Case 1
: If we use a telecentric system, then the
field angle is 0 all over the field of view. This is nice since the CWL
shift and the FWHM broadening will be constant all over the field of
view, their value will be depend on the f-ratio of the instrument.
Obviously, this is the optimal situation when using a F-P etalon at the
focus
of instrument. The CWL blue shift is equal to half the D FWHM.
We can notice that in a non telecentric system the field angle is equal to 0 only on the optical axis.
- Case 2 and 3 : If we don't use a telecentric system
(or if the telecentric system is not optimised for the focal length of
the telescope), then we have a field angle, which could be lower (case
2) or greater (case 3) than the cone half angle.
Accuracy of these formulae:
The accuracy of these formulae has been checked by comparison to the
calculation by integration of the Lorentzian function over the pupil of
the telescope in different situations (telecentric beam, non
telecentric beam with/without filter tilt, non telecentric beam with
Barlow lens with/without filter tilt).
The accuracy of the formulae
is quite good for telecentric beams with f-ratio > 20, they
are in excellent
agreement (3-digit accuracy) with numerical calculations based on the
integration
of the
Lorentzian transmission function over the pupil of the telescope.
For optical system with a field angle and/or filter tilt, the accuracy is lower. Still results are quite usefull.
As an exemple, here is the FWHM broadening calculated with the
formulae for a mica-spaced etalon (assuming an index n = 1.6173) in a
telecentric beam:

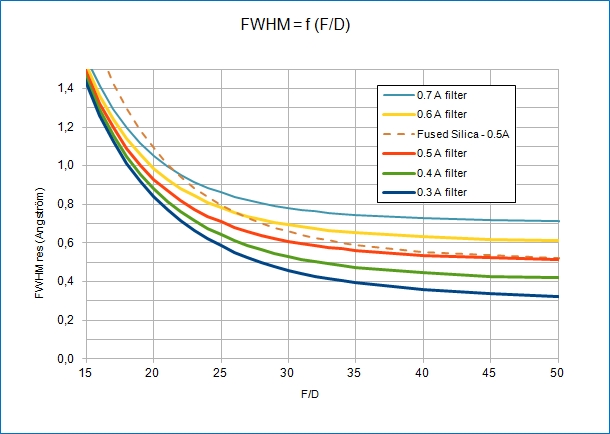
| Nominal FWHM |
Effective FWHM at F/30 |
FWHM broadening |
|
0.3 A
|
0.46 A
|
+0.16A
|
|
0.4 A
|
0.53 A
|
+ 0.13 A
|
|
0.5 A
|
0.61 A
|
+ 0.11 A
|
|
0.6 A
|
0.69 A
|
+ 0.09 A
|

















